【题目】有一个二次函数满足以下条件:
①函数图象与x轴的交点坐标分别为A(1,0),B(x2,y2)(点B在点A的右侧);
②对称轴是x=3;
③该函数有最小值是﹣2.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象x>x2的部分图象向下翻折与原图象未翻折的部分组成图象“G”,平行于x轴的直线与图象“G”相交于点C(x3,y3)、D(x4,y4)、E(x5,y5)(x3<x4<x5),结合画出的函数图象求x3+x4+x5的取值范围.
参考答案:
【答案】(1)y=![]() (x﹣3)2﹣2;(2)11<x3+x4+x5<9+2
(x﹣3)2﹣2;(2)11<x3+x4+x5<9+2![]() .
.
【解析】
(1)利用二次函数解析式的顶点式求得结果即可;
(2)由已知条件可知直线与图象“G”要有3个交点.分类讨论:分别求得平行于x轴的直线与图象“G”有2个交点、1个交点时x3+x4+x5的取值范围,易得直线与图象“G”要有3个交点时x3+x4+x5的取值范围.
(1)有上述信息可知该函数图象的顶点坐标为:(3,﹣2)
设二次函数表达式为:y=a(x﹣3)2﹣2.
∵该图象过A(1,0)
∴0=a(1﹣3)2﹣2,解得a=![]() .
.
∴表达式为y=![]() (x﹣3)2﹣2
(x﹣3)2﹣2
(2)如图所示:
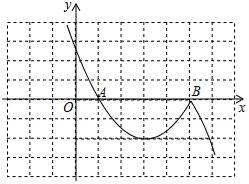
由已知条件可知直线与图形“G”要有三个交点
1当直线与x轴重合时,有2个交点,由二次函数的轴对称性可求x3+x4=6,
∴x3+x4+x5>11,
当直线过y=![]() (x﹣3)2﹣2的图象顶点时,有2个交点,
(x﹣3)2﹣2的图象顶点时,有2个交点,
由翻折可以得到翻折后的函数图象为y=﹣![]() (x﹣3)2+2,
(x﹣3)2+2,
∴令![]() (x﹣3)2+2=﹣2时,解得x=3+2
(x﹣3)2+2=﹣2时,解得x=3+2![]() 或x=3﹣2
或x=3﹣2![]() (舍去)
(舍去)
∴x3+x4+x5<9+2![]() .
.
综上所述11<x3+x4+x5<9+2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数
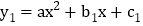 和
和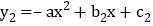 的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数
的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数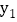 和
和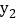 互为中心对称函数.
互为中心对称函数.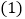 求函数
求函数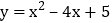 的中心对称函数;
的中心对称函数;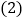 如图,在平面直角坐标系xOy中,E,F两点的坐标分别为
如图,在平面直角坐标系xOy中,E,F两点的坐标分别为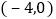 ,
,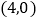 ,二次函数
,二次函数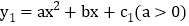 的图象经过点E和原点O,顶点为
的图象经过点E和原点O,顶点为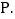 已知函数
已知函数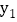 和
和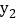 互为中心对称函数;
互为中心对称函数; 请在图中作出二次函数
请在图中作出二次函数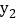 的顶点
的顶点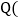 作图工具不限
作图工具不限 ,并画出函数
,并画出函数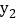 的大致图象;
的大致图象; 当四边形EPFQ是矩形时,请求出a的值;
当四边形EPFQ是矩形时,请求出a的值;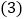 已知二次函数
已知二次函数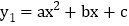 和
和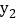 互为中心对称函数,且
互为中心对称函数,且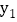 的图象经过
的图象经过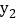 的顶点当
的顶点当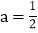 时,求代数式
时,求代数式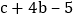 的最大值.
的最大值.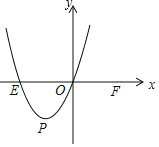
-
科目: 来源: 题型:
查看答案和解析>>【题目】亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,对于任意两点
 ,
, ,若点
,若点 满足
满足 ,
, 那么称点
那么称点 是点
是点 ,
, 的融合点,例如:
的融合点,例如: ,
, ,当点
,当点 满足
满足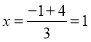 ,
, 时,则点
时,则点 是点
是点 ,
, 的融合点.
的融合点.(1)已知点
 ,
, ,
, ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.(2)如图,点
 ,点
,点 是直线
是直线 上任意一点,点
上任意一点,点 是点
是点 ,
, 的融合点.
的融合点.
①试确定
 与
与 的关系式;
的关系式;②在给定的坐标系
 中,画出①中的函数图象;
中,画出①中的函数图象;③若直线
 交
交 轴于点
轴于点 .当
.当 为直角三角形时,直接写出点
为直角三角形时,直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
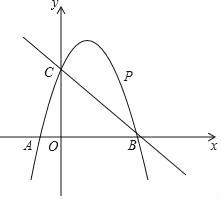
查看答案和解析>>【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
-
科目: 来源: 题型:
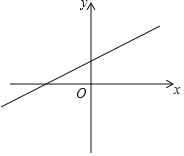
查看答案和解析>>【题目】如图,平面直角坐标系中,直线l:y=
 x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.
x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.(1)求点A的坐标;
(2)求此二次函数的解析式;
(3)点P为直线l上一动点,将线段AC绕点P顺时针旋转α°(0°<α°<360°)得到线段A'C'(点A,A'是对应点,点C,C'是对应点).请问:是否存在这样的点P,使得旋转后点A'和点C'分别落在直线l和抛物线y=ax2﹣3ax+c的图象上?若存在,请直接写出点A'的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线L1:y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,在L1上任取一点P,过点P作直线l⊥x轴,垂足为D,将L1沿直线l翻折得到抛物线L2,交x轴于点M,N(点M在点N的左侧).
(1)当L1与L2重合时,求点P的坐标;
(2)当点P与点B重合时,求此时L2的解析式;并直接写出L1与L2中,y均随x的增大而减小时的x的取值范围;
(3)连接PM,PB,设点P(m,n),当n=
 m时,求△PMB的面积.
m时,求△PMB的面积.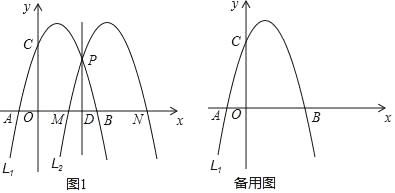
相关试题

