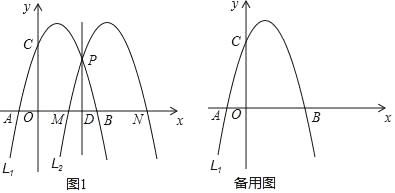
【题目】如图1,已知抛物线L1:y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,在L1上任取一点P,过点P作直线l⊥x轴,垂足为D,将L1沿直线l翻折得到抛物线L2,交x轴于点M,N(点M在点N的左侧).
(1)当L1与L2重合时,求点P的坐标;
(2)当点P与点B重合时,求此时L2的解析式;并直接写出L1与L2中,y均随x的增大而减小时的x的取值范围;
(3)连接PM,PB,设点P(m,n),当n=![]() m时,求△PMB的面积.
m时,求△PMB的面积.
参考答案:
【答案】(1)P(1,4);(2)x≥5 ;(3)△PMB的面积为![]() 或3
或3
【解析】
(1)由配方法可得顶点坐标;
(2)由对称性求出抛物线L2的顶点,进而得到解析式,由图象可得;
(3)利用点P在抛物线上和n=![]() m构造方程求出m、n,分类讨论求△PMB的面积.
m构造方程求出m、n,分类讨论求△PMB的面积.
(1)由抛物线对称性,当点P为抛物线L1的顶点时,抛物线L1与L2重合
∵y=-x2+2x+3=-(x-1)2+4
∴点P(1,4)
(2)在抛物线L1中,令y=0,即-x2+2x+3=0
解得x1=-1,x2=3
当点P与点B重合时,此时P(3,0)
∴抛物线L2与抛物线L1关于直线x=3对称
∴抛物线L2的顶点为(5,4)
∵由抛物线对称性可知,抛物线L1和L2开口方向和大小相同.
∴抛物线L2和的解析式为y=-(x-5)2+4=-x2+10x-21
∴结合图象可知,当x≥5时,抛物线L1与抛物线L2中,y均随x的增大而减小
(3)当n=![]() m时,-m2+2m+3=
m时,-m2+2m+3=![]() m
m
解得m1=-![]() ,m2=2
,m2=2
∴点P坐标为(-![]() ,-
,-![]() )或(2,3)
)或(2,3)
①如图1,
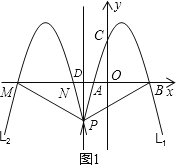
当点P坐标为(-![]() ,-
,-![]() )时,点D的坐标为坐标为(-
)时,点D的坐标为坐标为(-![]() ,0)
,0)
∴DB=3-(-![]() )=
)=![]()
∴MB=2BD=2×![]() =9
=9
∴S△PMB=![]() MBPD=
MBPD=![]() ×9×
×9×![]() =
=![]()
②如图2,

当点P坐标为(2,3)时,点D的坐标为坐标为(2,0)
∴DB=3-2=1
∴MB=2BD=2
∴S△PMB=![]() MBPD=
MBPD=![]() ×2×3=3
×2×3=3
综上所述当点n=![]() m时,△PMB的面积为
m时,△PMB的面积为![]() 或3.
或3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个二次函数满足以下条件:
①函数图象与x轴的交点坐标分别为A(1,0),B(x2,y2)(点B在点A的右侧);
②对称轴是x=3;
③该函数有最小值是﹣2.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象x>x2的部分图象向下翻折与原图象未翻折的部分组成图象“G”,平行于x轴的直线与图象“G”相交于点C(x3,y3)、D(x4,y4)、E(x5,y5)(x3<x4<x5),结合画出的函数图象求x3+x4+x5的取值范围.
-
科目: 来源: 题型:
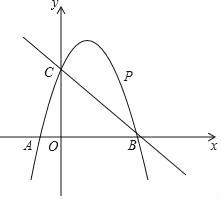
查看答案和解析>>【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
-
科目: 来源: 题型:
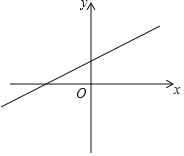
查看答案和解析>>【题目】如图,平面直角坐标系中,直线l:y=
 x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.
x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.(1)求点A的坐标;
(2)求此二次函数的解析式;
(3)点P为直线l上一动点,将线段AC绕点P顺时针旋转α°(0°<α°<360°)得到线段A'C'(点A,A'是对应点,点C,C'是对应点).请问:是否存在这样的点P,使得旋转后点A'和点C'分别落在直线l和抛物线y=ax2﹣3ax+c的图象上?若存在,请直接写出点A'的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰
 中,
中, ,
,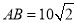 ,点
,点 为
为 的中点,点
的中点,点 在
在 上,
上, ,将线段
,将线段 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得到
得到 ,连接
,连接 ,然后把
,然后把 沿着
沿着 翻折得到
翻折得到 ,连接
,连接 ,
, ,取
,取 的中点
的中点 ,连接
,连接 ,则
,则 的长为( )
的长为( )
A.
 B.
B. C.2D.
C.2D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b'),给出如下定义:
若b'=
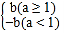 ,则称点Q为点P的限变点.例如:点(3,﹣2)的限变点的坐标是(3,﹣2),点(﹣1,5)的限变点的坐标是(﹣1,﹣5).
,则称点Q为点P的限变点.例如:点(3,﹣2)的限变点的坐标是(3,﹣2),点(﹣1,5)的限变点的坐标是(﹣1,﹣5).(1)①点(﹣
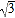 ,1)的限变点的坐标是 ;
,1)的限变点的坐标是 ;②在点A(﹣1,2),B(﹣2,﹣1)中有一个点是函数y=
 图象上某一个点的限交点,这个点是 ;
图象上某一个点的限交点,这个点是 ;(2)若点P在函数y=﹣x+3的图象上,当﹣2≤x≤6时,求其限变点Q的纵坐标b'的取值范围;
(3)若点P在关于x的二次函数y=x2﹣2tx+t2+t的图象上,其限变点Q的纵坐标b'的取值范围是b'≥m或b'<n,其中m>n.令s=m﹣n,求s关于t的函数解析式及s的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)已知直线l的解析式为y=kx﹣5.
(1)求抛物线L1的解析式、对称轴和顶点坐标.
(2)若直线l将线段AB分成1:3两部分,求k的值;
(3)当k=2时,直线与抛物线交于M、N两点,点P是抛物线位于直线上方的一点,当△PMN面积最大时,求P点坐标,并求面积的最大值.
(4)将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方,将这部分图象与原抛物线剩余的部分组成的新图象记为L2
①直接写出y随x的增大而增大时x的取值范围;
②直接写出直线l与图象L2有四个交点时k的取值范围.

相关试题

