【题目】如图,某农场老板准备建造一个矩形羊圈ABCD,他打算让矩形羊圈的一面完全靠着墙MN,墙MN可利用的长度为25m,另外三面用长度为50m的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)
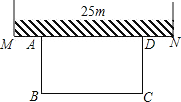
(1)若要使矩形羊圈的面积为300m2,则垂直于墙的一边长AB为多少米?
(2)农场老板又想将羊圈ABCD的面积重新建造成面积为320m2,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
参考答案:
【答案】(1)15米.(2)不能,理由见解析
【解析】
试题分析:(1)设所围矩形ABCD的宽AB为x米,则宽AD为(50﹣2x)米,根据矩形面积的计算方法列出方程求解.
(2)假使矩形面积为320,则x无实数根,所以不能围成矩形场地.
解:(1)设所围矩形ABCD的宽AB为x米,则宽AD为(50﹣2x)米.
依题意,得x(50﹣2x)=300,
即,x2﹣25x+150=0,
解此方程,得x1=15,x2=10.
∵墙的长度不超过25m,
∴x2=10不合题意,应舍去.
∴垂直于墙的一边长AB为15米.
(2)不能.
因为由x(50﹣2x)=320得x2﹣25x+160=0(6分).
又∵b2﹣4ac=(25)2﹣4×1×160=﹣15<0,
∴上述方程没有实数根.
因此,不能使所围矩形场地的面积为320m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-3a2(ab)2
(2)x(y-5)+y(3-x)
(3)(x+2)(x-1)-3x(x+1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=1,AD=
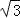 ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )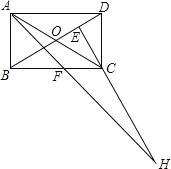
A.②③ B.③④ C.①②④ D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(m+1)x3m-2+3=0是一元一次方程,则m2+3m-2的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能化简(x-1)(x99+x98+x97+…+x+1)吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手,然后归纳出一些方法.
(1)分别化简下列各式:
①(x-1)(x+1)=___________;
②(x-1)(x2+x+1)=___________;
③(x-1)(x3+x2+1)=___________;
……
由此我们可以得到:(x-1)(x99+x98+x97+…+x+1)=________________.
(2)请你利用上面的结论计算:
299+298+297+…+2+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80,求∠BPC= .
(2)如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示) .
(3)将直线MN绕点P旋转。
(i)当直线MN与AB,AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。

-
科目: 来源: 题型:
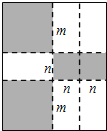
查看答案和解析>>【题目】
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.
(1)用含m、n的代数式表示切痕的总长为_____________厘米;
(2)若每块小矩形的面积为48厘米2,四个正方形的面积和为200厘米2,试求(m+n)2的值.
相关试题

