搜索
【题目】已知：如图，△ABC中，AB=AC，∠B、∠C的平分线相交于点O，过点O作EF∥BC交AB、AC于E、F．求证：EF=BE+CF．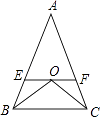 
参考答案：
【答案】证明：∵BO为∠ABC的平分线， ∴∠EBO=∠CBO，
又∵EF∥BC，
∴∠EOB=∠CBO，
∴∠EBO=∠EOB，
∴EB=EO，
同理FC=FO，
又∵EF=EO+OF，
∴EB+FC=EO+OF=EF
【解析】由BO为角平分线，利用角平分线的性质得到一对角相等，再由EF与BC平行，利用两直线平行内错角相等得到一对角相等，等量代换可得出∠EBO=∠EOB，利用等角对等边得到EB=EO，同理得到FC=FO，再由EF=EO+OF，等量代换可得证．
【考点精析】解答此题的关键在于理解平行线的性质的相关知识，掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（12分）实施新课程改革后，学生的自主学习、合作交流能力有很大提高，张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期三个月的跟踪调查，并将调查结果分成四类，A：特别好；B：好；C：一般；D：较差；并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：
（1）本次调查中，张老师一共调查了 名同学，其中C类女生有 名，D类男生有 名；
（2）将上面的条形统计图补充完整；
（3）为了共同进步，张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算下列各题
（1）计算：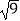
+ 
﹣ 
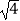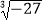
（2）求x的值：4x2﹣36=0． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，半径为1个单位的圆片上有一点Q与数轴上的原点重合（提示：圆的周长C=2πr，本题中π的取值为3.14）
（1）把圆片沿数轴向右滚动1周，点Q到达数轴上点A的位置，则点A表示的数是 。
（2）圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动的情况记录如下：+2，-1，-5，+4，+3，-2.
①第几次滚动后，Q点距离原点最近？第几次滚动后，Q点距离原点最远？
②当圆片结束运动后，Q点运动的路程共有多少？此时点Q所表示的数是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两上数的和．现以这组数中的各个数作为正方形的边长构造如图1正方形：再分别依次从左到右取2个、3个、4个、5个正方形拼成如图2所示的长方形并记为①、②、③、④．若按此规律继续作长方形，则序号为⑧的长方形的周长是______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在每个小正方形的边长为1的网格中，每个小正方形的顶点称为格点．我们将从一个格点移动到与之相距
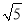的另一个格点的运动称为一次跳马变换．（1）在图1中画出边长为
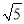的正方形，使它的顶点在网格的格点上． （2）在图2中有一只电子小马从格点
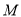出发，经过跳马变换到达与其相对的格点
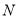，则最少需要跳马变换的次数是 次．（3）如图3，在
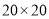的正方形网格中，一只电子小马从格点
经过若干次跳马变换到达与其相对的格点
，则它跳过的最短路程为 ．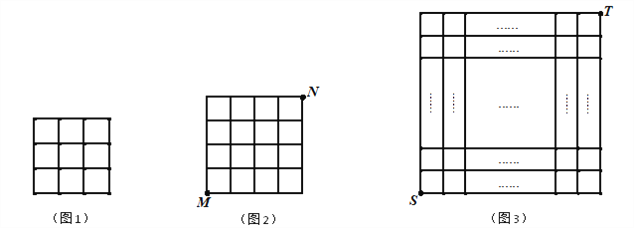
-
科目： 来源： 题型：
查看答案和解析>>【题目】“滴滴”已成为一种出行习惯，其中的“滴滴专车”正成为非常热门的出行选择．经了解温州地区滴滴专车部分计价规则如下表：
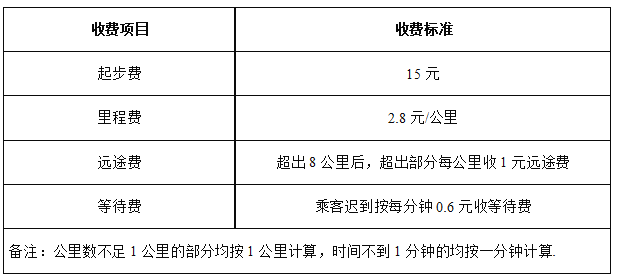
以没有收取等待费为例：某甲坐车10公里的费用为15+2.8×10+1×(10-8)=45元
（1）若行驶里程为6千米，且没有收取等待费，求应支付的总费用；
（2）若某天小周迟到7分钟才上车，且里程数超过了8公里，最终支付的总费用为53元，求支付的远途费；
（3）某次行程结束后，乘客小周发现乘车的里程数超过了5公里，需要支付的费用恰好为46元，起初小周认为系统计算错误，经司机提醒才记起，原来是他有事耽搁没有及时上车，被收取了等待费，则收取的等待费为 元．（直接在横线上写出答案）
相关试题
