【题目】在每个小正方形的边长为1的网格中,每个小正方形的顶点称为格点.我们将从一个格点移动到与之相距![]() 的另一个格点的运动称为一次跳马变换.
的另一个格点的运动称为一次跳马变换.
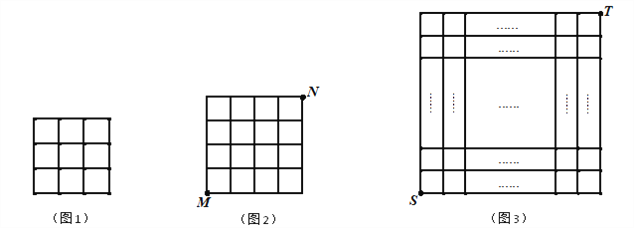
(1)在图1中画出边长为![]() 的正方形,使它的顶点在网格的格点上.
的正方形,使它的顶点在网格的格点上.
(2)在图2中有一只电子小马从格点![]() 出发,经过跳马变换到达与其相对的格点
出发,经过跳马变换到达与其相对的格点![]() ,则最少需要跳马变换的次数是 次.
,则最少需要跳马变换的次数是 次.
(3)如图3,在![]() 的正方形网格中,一只电子小马从格点
的正方形网格中,一只电子小马从格点![]() 经过若干次跳马变换到达与其相对的格点
经过若干次跳马变换到达与其相对的格点![]() ,则它跳过的最短路程为 .
,则它跳过的最短路程为 .
参考答案:
【答案】(1)作图见解析;(2)4;(3)14![]()
【解析】试题分析:(1).根据题意画出图形即可;(2).根据题意画出图形解答;(3)根据从一个格点移动到与之相距![]() 的另一个格点的运动称为一次跳马变换,计算出按A-C-F的方向连续变换10次后点S的位置,再根据点T的位置进行适当的变换,即可得到变换总次数.
的另一个格点的运动称为一次跳马变换,计算出按A-C-F的方向连续变换10次后点S的位置,再根据点T的位置进行适当的变换,即可得到变换总次数.
解:(1)如图1,
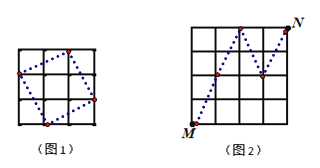
(2)如图2,最少需要跳马变换的次数是4次.
(3)如图3, ![]() ,
,
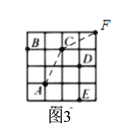
![]() 两次变换相当于向右移动3格,向上移动3格,
两次变换相当于向右移动3格,向上移动3格,
又∵![]() ,
,
![]() (不是整数),
(不是整数),
![]() 按A-C-F的方向连续变换10次后,相当于向右移动了10÷2×3=15格,向上移动了10÷2×3=15格,此时S位于如图所示的5×5的正方形网格的点G处,再按如图所示的方式变换4次即可到达点T处,
按A-C-F的方向连续变换10次后,相当于向右移动了10÷2×3=15格,向上移动了10÷2×3=15格,此时S位于如图所示的5×5的正方形网格的点G处,再按如图所示的方式变换4次即可到达点T处,
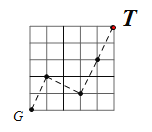
![]() 从该正方形的顶点S经过跳马变换到达与其相对的顶点T,最少需要跳马变换的次数是14次,
从该正方形的顶点S经过跳马变换到达与其相对的顶点T,最少需要跳马变换的次数是14次,
∴它跳过的最短路程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2πr,本题中π的取值为3.14)

(1)把圆片沿数轴向右滚动1周,点Q到达数轴上点A的位置,则点A表示的数是 。
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动的情况记录如下:+2,-1,-5,+4,+3,-2.
①第几次滚动后,Q点距离原点最近?第几次滚动后,Q点距离原点最远?
②当圆片结束运动后,Q点运动的路程共有多少?此时点Q所表示的数是多少?
-
科目: 来源: 题型:
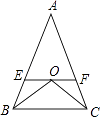
查看答案和解析>>【题目】已知:如图,△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.求证:EF=BE+CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两上数的和.现以这组数中的各个数作为正方形的边长构造如图1正方形:再分别依次从左到右取2个、3个、4个、5个正方形拼成如图2所示的长方形并记为①、②、③、④.若按此规律继续作长方形,则序号为⑧的长方形的周长是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“滴滴”已成为一种出行习惯,其中的“滴滴专车”正成为非常热门的出行选择.经了解温州地区滴滴专车部分计价规则如下表:
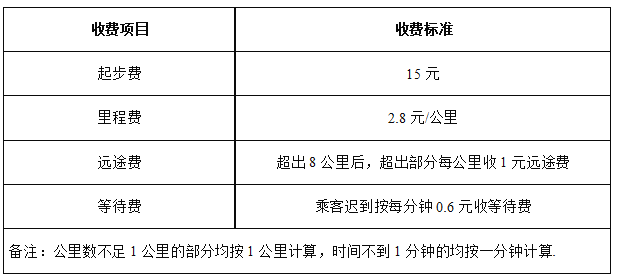
以没有收取等待费为例:某甲坐车10公里的费用为15+2.8×10+1×(10-8)=45元
(1)若行驶里程为6千米,且没有收取等待费,求应支付的总费用;
(2)若某天小周迟到7分钟才上车,且里程数超过了8公里,最终支付的总费用为53元,求支付的远途费;
(3)某次行程结束后,乘客小周发现乘车的里程数超过了5公里,需要支付的费用恰好为46元,起初小周认为系统计算错误,经司机提醒才记起,原来是他有事耽搁没有及时上车,被收取了等待费,则收取的等待费为 元.(直接在横线上写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组利用三角形相似测量学校旗杆的高度.测得身高为1.6米小明同学在阳光下的影长为1米,此时测得旗杆的影长为9米.则学校旗杆的高度是( )
A.9米B.14.4米C.16米D.13.4米
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1:
 :3,求∠AED的度数;
:3,求∠AED的度数;(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=
 ,求CN的长.
,求CN的长.
相关试题

