【题目】如图,将一条长为60cm的卷尺铺平后沿着图中箭头的方向折叠,使得卷尺自身的一部分重合,然后在重合部分沿与卷尺的边垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度比为1:2:3,则折痕对应的刻度可能的值有 ________.
![]()
参考答案:
【答案】20,25,35,40
【解析】试题解析:∵三段长度由短到长的比为1:2:3,
∴三段长度分别为:10cm,20cm,30cm.
①当剪切处右边上部分的长度为10cm,剪切处左边的卷尺为20cm时,
折痕处为:10+![]() =20cm;
=20cm;
②当剪切处右边上部分的长度为10cm,剪切处左边的卷尺为30cm时,
折痕处为:10+![]() =25cm;
=25cm;
③当剪切处右边上部分的长度为20cm,剪切处左边的卷尺为10cm时,
折痕处为:20+![]() =25cm;
=25cm;
④当剪切处右边上部分的长度为20cm,剪切处左边的卷尺为30cm时,
折痕处为:20+![]() =35cm;
=35cm;
⑤当剪切处右边上部分的长度为30cm,剪切处左边的卷尺为10cm时,
折痕处为:30+![]() =35cm;
=35cm;
⑥当剪切处右边上部分的长度为30cm,剪切处左边的卷尺为20cm时,
折痕处为:30+![]() =40cm;
=40cm;
综上所述,折痕对应的刻度有4种可能:20cm,25cm,35cm,40cm.
故答案为:20cm,25cm,35cm,40cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在某分期比赛中有A、B、C三组家庭进行比赛:
(1)选手选择A组家庭的宝宝,在妈妈区域中正确找出其妈妈的概率为 ;
(2)如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求选手至少正确找对宝宝父母其中一人的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+2与x轴、y轴分别交于点A、B,点C(1,a)是该直线与双曲线y=
 的一个交点,过点C作CD垂直y轴,垂足为D,且S△BCD=1.
的一个交点,过点C作CD垂直y轴,垂足为D,且S△BCD=1.
(1)求双曲线的解析式.
(2)设直线与双曲线的另一个交点为E,求点E的坐标.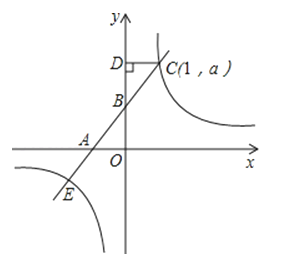
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=mx+4的图象与x轴相交于点A,与反比例函数y=
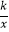
 的图象相交于点B(1,6).
的图象相交于点B(1,6).
(1)求一次函数和反比例函数的解析式;
(2)设点P是x轴上一点,若S△APB=18,直接写出点P的坐标.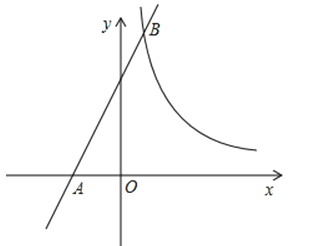
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=3是关于x的方程x2+kx﹣6=0的一个根,则另一个根是( )
A.x=1B.x=﹣2C.x=﹣1D.x=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(3a2-8a)+(2a3-13a2+2a)-2(a3-3),其中a=-4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数:
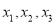 ,称为数列
,称为数列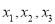 .计算
.计算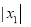 ,
, 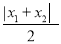 ,
, 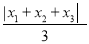 将这三个数的最小值称为数列
将这三个数的最小值称为数列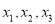 的价值.例如,对于数列2,﹣1,3,因为
的价值.例如,对于数列2,﹣1,3,因为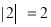 ,
, 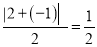 ,
, 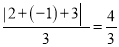 ,所以数列2,﹣1,3的价值为
,所以数列2,﹣1,3的价值为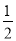 .
.小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列﹣1,2,3的价值为
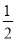 ;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为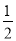 .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:(1)数列﹣4,﹣3,2的价值为 ;
(2)将“﹣4,﹣3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为 ,取得价值最小值的数列为 (写出一个即可);
(3)将2,﹣9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为 .
相关试题

