【题目】(12分)如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
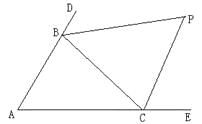
(1)若∠A=50°,则∠P= °;
(2)若∠A=90°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系,并说明理由。
参考答案:
【答案】解:(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,∠DBC+∠BCE=360°-130°=230°,
又∵∠CBD与∠BCE的平分线相交于点P,
∴∠PBC=![]() ∠DBC,∠PCB=
∠DBC,∠PCB=![]() ∠ECB,
∠ECB,
∴∠PBC+∠PCB=![]() (∠DBC+∠ECB)=115°,
(∠DBC+∠ECB)=115°,
∴∠P=65°.
同理得:(2)45°;
(3)40°
(4)∠P=90°-![]() ∠A.理由如下:
∠A.理由如下:
∵BP平分∠DBC,CP平分∠BCE,
∴∠DBC=2∠CBP,∠BCE=2∠BCP
又∵∠DBC=∠A+∠ACB∠BCE=∠A+∠ABC,
∴2∠CBP=∠A+∠ACB,2∠BCP=∠A+∠ABC,
∴2∠CBP+2∠BCP=∠A+∠ACB+∠A+∠ABC=180°+∠A,
∴∠CBP+∠BCP=90°+![]() ∠A
∠A
又∵∠CBP+∠BCP+∠P=180°,
∴∠P=90°-![]() ∠A.
∠A.
【解析】试题分析:(1)若∠A=50°,则有∠ABC+∠ACB=130°,∠DBC+∠BCE=360°-130°=230°,根据角平分线的定义可以求得∠PBC+∠PCB的度数,再利用三角形的内角和定理即可求得∠P的度数;
(2)、(3)和(1)的解题步骤类似;(4)利用角平分线的性质和三角形的外角性质可求出∠BCP=![]() (∠A+∠ABC),∠CBP=
(∠A+∠ABC),∠CBP=![]() (∠A+∠ACB);再利用三角形内角和定理即可求出∠A与∠P的关系.
(∠A+∠ACB);再利用三角形内角和定理即可求出∠A与∠P的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a2+a=a3 B. a2a=a3 C. a2÷a=2 D. (2a)2=4a
-
科目: 来源: 题型:
查看答案和解析>>【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=
 ,b=
,b=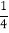 ,c=
,c= ②a=6,∠A=45°; ③∠A=32°,∠B=58°;
②a=6,∠A=45°; ③∠A=32°,∠B=58°; ④a=7,b=24,c=25 ⑤a=2,b=2,c=4.
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若将左图正方形剪成四块,恰能拼成右图的矩形,设a=1,则b=( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下可以用来说明命题“任何奇数都是3的倍数”是假命题的反例是( )
A.9
B.7
C.8
D.15 -
科目: 来源: 题型:
查看答案和解析>>【题目】若点M在第一、三象限的角平分线上,且点M到x轴的距离为2,则点M的坐标是( )
A. (2,2) B. (-2,-2) C. (2,2)或(-2,-2) D. (2,-2)或(-2,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的三边长分别为6、8、10,则这个三角形最长边上的中线长为( )
A.3.6 B.4 C.4.8 D.5
相关试题

