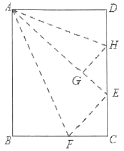
【题目】在数学拓展课上,小林发现折叠长方形纸片ABCD可以进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕为AF,点F在BC边上;②把△ADH翻折,点D落在AE边上的点G处,折痕为AH,点H在CD边上.若AD=6,AB=![]() 则∠HAF=___,GE=___.
则∠HAF=___,GE=___.
参考答案:
【答案】45°, 14-a
【解析】
由折叠的性质可得AB=AE=20-a,AD=AG=6,可求GE的长,再根据∠DAH=∠GAH,∠BAF=∠EAF,且∠DAH+∠GAH+∠BAF+∠EAF=90°,即可求出∠HAF的度数.
解:由折叠的性质可得:△ABF≌△AEF,△ADH≌△AGH
∴AB=AE=20-a,AD=AG=6,∠DAH=∠GAH,∠BAF=∠EAF
∴GE=AE-AG=20-a-6=14-a,
∵∠DAH+∠GAH+∠BAF+∠EAF=90°
∴2∠GAH+2∠EAF=90°
∴∠GAH+∠EAF=45°
∴∠HAF=45°
故答案为:45°,14-a,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.

(1)若AC=9cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并直接写出你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
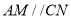 ,点
,点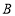 为平面内一点,
为平面内一点,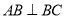 于
于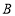 .
.(1)如图1,直接写出
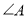 和
和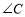 之间的数量关系 ;
之间的数量关系 ;(2)如图2,过点
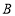 作
作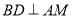 于点
于点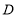 ,求证:
,求证: ;
;(3)如图3,在(2)问的条件下,点
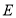 、
、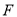 在
在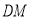 上,连接
上,连接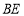 、
、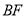 、
、 ,
,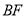 平分
平分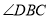 ,
,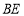 平分
平分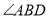 ,若
,若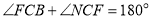 ,
,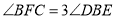 ,求
,求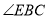 的度数.
的度数.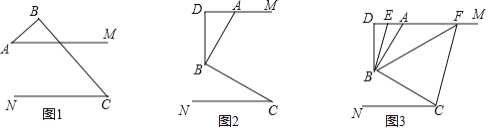
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将
 化为分数形式
化为分数形式由于
 =0.777…,设x=0.777…①
=0.777…,设x=0.777…①则10x=7.777…②
②﹣①得9x=7,解得x=
 ,于是得
,于是得 =
= .
.同理可得
 =
= ,
, =1+
=1+ =1+
=1+ ,
,根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(基础训练)
(1)
 = ,
= , = ;
= ;(2)将
 化为分数形式,写出推导过程;
化为分数形式,写出推导过程;(能力提升)
(3)
 = ,
= , = ;
= ;(注:
 =0.315315…,
=0.315315…, =2.01818…)
=2.01818…)(探索发现)
(4)①试比较
 与1的大小:
与1的大小: 1(填“>”、“<”或“=”)
1(填“>”、“<”或“=”)②若已知
 =
= ,则
,则 = .
= .(注:
 =0.285714285714…)
=0.285714285714…) -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂加工螺栓、螺帽,已知每1块金属原料可以加工成3个螺栓或4个螺帽(说明:每块金属原料无法同时既加工螺栓又加工螺帽),已知1个螺栓和2个螺帽组成一个零件,为了加工更多的零件,要求螺栓和螺帽恰好配套.请列方程解决下列问题:
(1)现有20块相同的金属原料,问最多能加工多少个这样的零件?
(2)若把26块相同的金属原料全部加工完,问加工的螺栓和螺帽恰好配套吗?说明理由
(3)若把
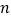 块相同的金属原料全部加工完,为了使这样加工出来的螺栓与螺帽恰好配套,请求出
块相同的金属原料全部加工完,为了使这样加工出来的螺栓与螺帽恰好配套,请求出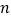 所满足的条件.
所满足的条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】每年的4月23日是“世界读书日”.某中学为了了解八年级学生的读书情况,随机调查了50名学生的册数,统计数据如表所示:
册数
0
1
2
3
4
人数
3
13
16
17
1
则这50名学生读数册数的众数、中位数是( )
A.3,3
B.3,2
C.2,3
D.2,2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有__________.(选序号)
①若
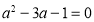 ,则
,则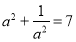 ;
;②若
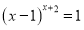 ,则满足条件
,则满足条件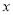 的值有3个;
的值有3个;③若
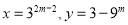 ,则用含
,则用含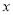 的代数式表示
的代数式表示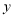 为
为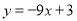 ;
;④若
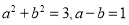 ,则
,则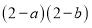 的值为
的值为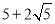 .
.
相关试题

