【题目】甲乙两同学用两枚质地均匀的骰子作游戏,规则如下:每人随机掷两枚骰子一次(若掷出的两枚骰子摞在一起,则重掷),点数和大的获胜;点数和相同为平局. 根据上述规则,解答下列问题;
(1)随机掷两枚骰子一次,用列表法求点数和为8的概率;
(2)甲先随机掷两枚骰子一次,点数和是7,求乙随机掷两枚骰子一次获胜的概率. (骰子:六个面分别有1、2、3、4、5、6个小圆点的立方块.点数和:两枚骰子朝上的点数之和)
参考答案:
【答案】
(1)解:画树状图为:
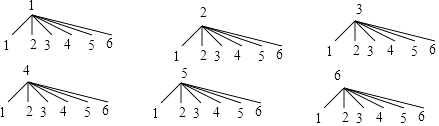
共有36种等可能的结果数,其中点数和为8的结果数为5,
点数和为8的概率= ![]()
(2)解:点数和大于7的结果数为15,
所以乙随机掷两枚骰子一次获胜的概率= ![]() =
= ![]()
【解析】(1)画树状图展示所有36种等可能的结果数,再找出点数和为8的结果数,然后根据概率公式求解;(2)找出点数和大于7的结果数,然后根据概率公式求解.
【考点精析】解答此题的关键在于理解列表法与树状图法的相关知识,掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,已知点O(0,0),A(1,0),B(1,1),C(2,0),△OBC的面积记为S1 , 过O、B、C三点的半圆面积记为S2;过O、B、C三点的抛物线与x轴所围成的图形面积记为S3 , 则S1、S2、S3的大小关系是 . (用“>”连接)
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数. 小颖同学的解题思路是:如图2,过点P作PE∥AB,请你接着完成解答.

问题迁移:
(2)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?

(提示:过点P作PE∥AD),请说明理由;
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你猜想∠CPD、∠α、∠β之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移得到△A1B1C1,且点P的对应点为P1(a+5,b+4).
(1)写出△A1B1C1的三个顶点的坐标;
(2)求△ABC的面积;
(3)请在平面直角坐标系中画出△A1B1C1.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度的速度都是1 cm/s,连结PQ,AQ,CP,设点P,Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课中,小辉将边长为
 和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.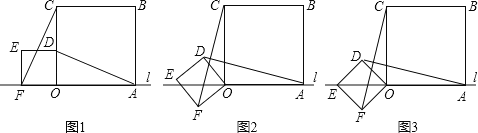
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.

相关试题

