【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为 ![]() .
.
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)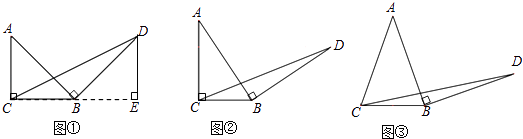
参考答案:
【答案】解:初步探究:△BCD的面积为 ![]() . 理由:如图②,过点D作BC的垂线,与BC的延长线交于点E.
. 理由:如图②,过点D作BC的垂线,与BC的延长线交于点E.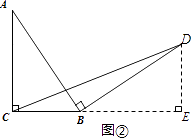
∴∠BED=∠ACB=90°.
∵线段AB绕点B顺时针旋转90°得到线段BE,
∴AB=BD,∠ABD=90°.
∴∠ABC+∠DBE=90°.
∵∠A+∠ABC=90°.
∴∠A=∠DBE.
在△ABC和△BDE中,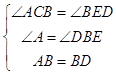 ,
,
∴△ABC≌△BDE(AAS)
∴BC=DE=a.
∵S△BCD= ![]() BCDE
BCDE
∴S△BCD= ![]() ;
;
简单应用:如图③,过点A作AF⊥BC与F,过点D作DE⊥BC的延长线于点E,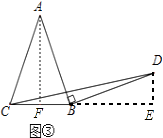
∴∠AFB=∠E=90°,BF= ![]() BC=
BC= ![]() a.
a.
∴∠FAB+∠ABF=90°.
∵∠ABD=90°,
∴∠ABF+∠DBE=90°,
∴∠FAB=∠EBD.
∵线段BD是由线段AB旋转得到的,
∴AB=BD.
在△AFB和△BED中,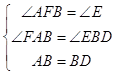 ,
,
∴△AFB≌△BED(AAS),
∴BF=DE= ![]() a.
a.
∵S△BCD= ![]() BCDE,
BCDE,
∴S△BCD= ![]()
![]() aa=
aa= ![]() a2 .
a2 .
∴△BCD的面积为 ![]() .
.
【解析】初步探究:如图②,过点D作BC的垂线,与BC的延长线交于点E,由垂直的性质就可以得出△ABC≌△BDE,就有DE=BC=a.进而由三角形的面积公式得出结论; 简单运用:如图③,过点A作AF⊥BC与F,过点D作DE⊥BC的延长线于点E,由等腰三角形的性质可以得出BF= ![]() BC,由条件可以得出△AFB≌△BED就可以得出BF=DE,由三角形的面积公式就可以得出结论.
BC,由条件可以得出△AFB≌△BED就可以得出BF=DE,由三角形的面积公式就可以得出结论.
【考点精析】本题主要考查了旋转的性质的相关知识点,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示. AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601,
 ≈1.414].
≈1.414].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为菱形ABCD对角线的交点,DE∥AC,CE∥BD.
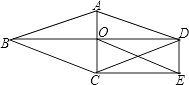
(1)试判断四边形OCED的形状,并说明理由;
(2)若AC=6,BD=8,求线段OE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两支清雪队同时开始清理某路段积雪,一段时间后,乙队被调往别处,甲队又用了3小时完成了剩余的清雪任务,已知甲队每小时的清雪量保持不变,乙队每小时清雪50吨,甲、乙两队在此路段的清雪总量y(吨)与清雪时间x(时)之间的函数图象如图所示.
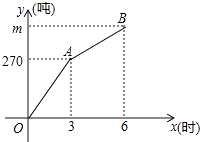
(1)乙队调离时,甲、乙两队已完成的清雪总量为吨;
(2)求此次任务的清雪总量m;
(3)求乙队调离后y与x之间的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC , BD相交于点O , 且AC=6cm,BD=8cm,动点P , Q分别从点B , D同时出发,运动速度均为1cm/s,点P沿B→C→D运动,到点D停止,点Q沿D→O→B运动,到点O停止1s后继续运动,到点B停止,连接AP , AQ , PQ . 设△APQ的面积为y(cm2)(这里规定:线段是面积0的几何图形),点P的运动时间为x(s).

(1)填空:AB=cm,AB与CD之间的距离为cm;
(2)当4≤x≤10时,求y与x之间的函数解析式;
(3)直接写出在整个运动过程中,使PQ与菱形ABCD一边平行的所有x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )

A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=
 的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.3
B.﹣3
C.6
D.﹣6
相关试题

