【题目】如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y= ![]() 的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.3
B.﹣3
C.6
D.﹣6
参考答案:
【答案】D
【解析】解:连接AC交OB于点D,如图所示. ∵四边形OABC为菱形,
∴AC⊥OB,
∵菱形OABC的面积为12,
∴SOCD= ![]() ×12=3.
×12=3.
∵点C在反比例函数y= ![]() 的图象上,CD⊥y轴,
的图象上,CD⊥y轴,
∴SOCD= ![]() |k|=3,
|k|=3,
解得:k=±6.
∵点C在第二象限,
∴k=﹣6.
故选D.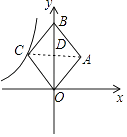
【考点精析】本题主要考查了比例系数k的几何意义和菱形的性质的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为
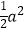 .
.
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC , BD相交于点O , 且AC=6cm,BD=8cm,动点P , Q分别从点B , D同时出发,运动速度均为1cm/s,点P沿B→C→D运动,到点D停止,点Q沿D→O→B运动,到点O停止1s后继续运动,到点B停止,连接AP , AQ , PQ . 设△APQ的面积为y(cm2)(这里规定:线段是面积0的几何图形),点P的运动时间为x(s).

(1)填空:AB=cm,AB与CD之间的距离为cm;
(2)当4≤x≤10时,求y与x之间的函数解析式;
(3)直接写出在整个运动过程中,使PQ与菱形ABCD一边平行的所有x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )

A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的
 倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大  倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
其中正确的是 .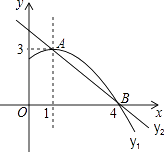
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△PAB中,∠APB=120°,M,N是AB上两点,且△PMN是等边三角形,求证:BMPA=PNBP.

相关试题

