【题目】如图,菱形ABCD中,对角线AC , BD相交于点O , 且AC=6cm,BD=8cm,动点P , Q分别从点B , D同时出发,运动速度均为1cm/s,点P沿B→C→D运动,到点D停止,点Q沿D→O→B运动,到点O停止1s后继续运动,到点B停止,连接AP , AQ , PQ . 设△APQ的面积为y(cm2)(这里规定:线段是面积0的几何图形),点P的运动时间为x(s). 
(1)填空:AB=cm,AB与CD之间的距离为cm;
(2)当4≤x≤10时,求y与x之间的函数解析式;
(3)直接写出在整个运动过程中,使PQ与菱形ABCD一边平行的所有x的值.
参考答案:
【答案】
(1)5;![]()
(2)解:设∠CBD=∠CDB=θ,则易得:sinθ= ![]() ,cosθ=
,cosθ= ![]() .
.

①当4≤x≤5时,如答图1﹣1所示,此时点Q与点O重合,点P在线段BC上.
∵PB=x,
∴PC=BC﹣PB=5﹣x.
过点P作PH⊥AC于点H,则PH=PCcosθ= ![]() (5﹣x).
(5﹣x).
∴y=S△APQ= ![]() QAPH=
QAPH= ![]() ×3×
×3× ![]() (5﹣x)=﹣
(5﹣x)=﹣ ![]() x+6;
x+6;
②当5<x≤9时,如答图1﹣2所示,此时点Q在线段OB上,点P在线段CD上.
PC=x﹣5,PD=CD﹣PC=5﹣(x﹣5)=10﹣x.
过点P作PH⊥BD于点H,则PH=PDsinθ= ![]() (10﹣x).
(10﹣x).
∴y=S△APQ=S菱形ABCD﹣S△ABQ﹣S四边形BCPQ﹣S△APD
=S菱形ABCD﹣S△ABQ﹣(S△BCD﹣S△PQD)﹣S△APD
= ![]() ACBD﹣
ACBD﹣ ![]() BQOA﹣(
BQOA﹣( ![]() BDOC﹣
BDOC﹣ ![]() QDPH)﹣
QDPH)﹣ ![]() PD×h
PD×h
= ![]() ×6×8﹣
×6×8﹣ ![]() (9﹣x)×3﹣[
(9﹣x)×3﹣[ ![]() ×8×3﹣
×8×3﹣ ![]() (x﹣1)
(x﹣1) ![]() (10﹣x)]﹣
(10﹣x)]﹣ ![]() (10﹣x)×
(10﹣x)× ![]()
=﹣ ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ;
;
③当9<x≤10时,如答图1﹣3所示,此时点Q与点B重合,点P在线段CD上.
y=S△APQ= ![]() AB×h=
AB×h= ![]() ×5×
×5× ![]() =12.
=12.
综上所述,当4≤x≤10时,y与x之间的函数解析式为:
y= 
(3)解:有两种情况:

①若PQ∥CD,如答图2﹣1所示.
此时BP=QD=x,则BQ=8﹣x.
∵PQ∥CD,
∴ ![]() ,
,
即 ![]() ,
,
∴x= ![]() ;
;
②若PQ∥BC,如答图2﹣2所示.
此时PD=10﹣x,QD=x﹣1.
∵PQ∥BC,
∴ ![]() ,
,
即 ![]() ,
,
∴x= ![]() .
.
综上所述,满足条件的x的值为 ![]() 或
或 ![]() .
.
【解析】解:(1)∵菱形ABCD中,AC=6cm,BD=8cm, ∴AC⊥BD,
∴AB= ![]() =
= ![]() =5,
=5,
设AB与CD间的距离为h,
∴△ABC的面积S= ![]() ABh,
ABh,
又∵△ABC的面积S= ![]() S菱形ABCD=
S菱形ABCD= ![]() ×
× ![]() ACBD=
ACBD= ![]() ×6×8=12,
×6×8=12,
∴ ![]() ABh=12,
ABh=12,
∴h= ![]() =
= ![]() .
.
(1)根据勾股定理即可求得AB,根据面积公式求得AB与CD之间的距离.(2)当4≤x≤10时,运动过程分为三个阶段,需要分类讨论,避免漏解:①当4≤x≤5时,如答图1﹣1所示,此时点Q与点O重合,点P在线段BC上;②当5<x≤9时,如答图1﹣2所示,此时点Q在线段OB上,点P在线段CD上;③当9<x≤10时,如答图1﹣3所示,此时点Q与点B重合,点P在线段CD上.(3)有两种情形,需要分类讨论,分别计算:①若PQ∥CD,如答图2﹣1所示;②若PQ∥BC,如答图2﹣2所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为菱形ABCD对角线的交点,DE∥AC,CE∥BD.
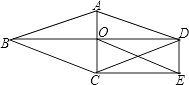
(1)试判断四边形OCED的形状,并说明理由;
(2)若AC=6,BD=8,求线段OE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两支清雪队同时开始清理某路段积雪,一段时间后,乙队被调往别处,甲队又用了3小时完成了剩余的清雪任务,已知甲队每小时的清雪量保持不变,乙队每小时清雪50吨,甲、乙两队在此路段的清雪总量y(吨)与清雪时间x(时)之间的函数图象如图所示.
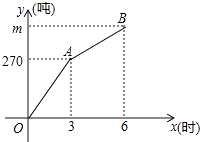
(1)乙队调离时,甲、乙两队已完成的清雪总量为吨;
(2)求此次任务的清雪总量m;
(3)求乙队调离后y与x之间的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为
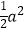 .
.
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)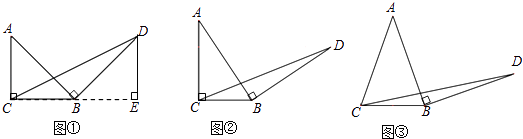
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )

A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=
 的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.3
B.﹣3
C.6
D.﹣6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的
 倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大  倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 . 
相关试题

