Question

【题目】在平面直角坐标系XOY中，直线l1过点A（1，0）且与y轴平行，直线l2过点B（0，2）且与x轴平行，直线l1与直线l2相交于点P．点E为直线l2上一点，反比例函数 （k＞0）的图象过点E与直线l1相交于点F．
（1）若点E与点P重合，求k的值；
（2）连接OE、OF、EF．若k＞2，且△OEF的面积为△PEF的面积的2倍，求E点的坐标；
（3）是否存在点E及y轴上的点M，使得以点M、E、F为顶点的三角形与△PEF全等？若存在，求E点坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）解：若点E与点P重合，则k=1×2=2
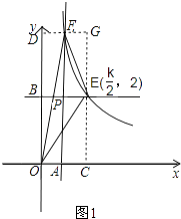
（2）解：当k＞2时，如图1，

点E、F分别在P点的右侧和上方，过E作x轴的垂线EC，垂足为C，过F作y轴的垂线FD，垂足为D，EC和FD相交于点G，则四边形OCGD为矩形，

∵PF⊥PE，

∴S△FPE= PEPF= （ ﹣1）（k﹣2）= k2﹣k+1，

∴四边形PFGE是矩形，

∴S△PFE=S△GEF，

∴S△OEF=S矩形OCGD﹣S△DOF﹣S△EGF﹣S△OCE= k﹣ ﹣（ k2﹣k+1）﹣ = k2﹣1，

∵S△OEF=2S△PEF，

∴ k2﹣1=2（ k2﹣k+1），

解得k=6或k=2，

∵k=2时，E、F重合，

∴k=6，

∴E点坐标为：（3，2）

（3）解：存在点E及y轴上的点M，使得△MEF≌△PEF，

①当k＜2时，如图2，只可能是△MEF≌△PEF，作FH⊥y轴于H，

∵∠MHF=∠EBM=90°，∠HMF=∠MEB，

∴△FHM∽△MBE，

∴ = ，

∵FH=1，EM=PE=1﹣ ，FM=PF=2﹣k，

∴ = ，BM= ，

在Rt△MBE中，由勾股定理得，EM2=EB2+MB2，

∴（1﹣ ）2=（ ）2+（ ）2，

解得k= ，此时E点坐标为（ ，2），

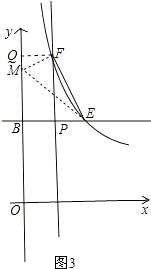
①当k＞2时，如图3，

只可能是△MFE≌△PEF，作FQ⊥y轴于Q，△FQM∽△MBE得， = ，

∵FQ=1，EM=PF=k﹣2，FM=PE= ﹣1，

∴ = ，BM=2，

在Rt△MBE中，由勾股定理得，EM2=EB2+MB2，

∴（k﹣2）2=（ ）2+22，解得k= 或0，但k=0不符合题意，

∴k= ．

此时E点坐标为（ ，2），

∴符合条件的E点坐标为（ ，2）（ ，2）．

【解析】（1）根据反比例函数中k=xy进行解答即可；（2）当k＞2时，点E、F分别在P点的右侧和上方，过E作x轴的垂线EC，垂足为C，过F作y轴的垂线FD，垂足为D，EC和FD相交于点G，则四边形OCGD为矩形，再求出S△FPE= k2﹣k+1，根据S△OEF=S矩形OCGD﹣S△DOF﹣S△EGF﹣S△OCE即可求出k的值，进而求出E点坐标；（3）①当k＜2时，只可能是△MEF≌△PEF，作FH⊥y轴于H，由△FHM∽△MBE可求出BM的值，再在Rt△MBE中，由勾股定理得，EM2=EB2+MB2 ， 求出k的值，进而可得出E点坐标； ②当k＞2时，只可能是△MFE≌△PEF，作FQ⊥y轴于Q，△FQM∽△MBE得， = ，可求出BM的值，再在Rt△MBE中，由勾股定理得，EM2=EB2+MB2 ， 求出k的值，进而可得出E点坐标．