【题目】如图,已知函数y= ![]() 与y=ax2+bx(a>0,b>0)的图象交于点P.点P的纵坐标为1.则关于x的方程ax2+bx+
与y=ax2+bx(a>0,b>0)的图象交于点P.点P的纵坐标为1.则关于x的方程ax2+bx+ ![]() =0的解为 .
=0的解为 . 
参考答案:
【答案】x=﹣3
【解析】解:∵P的纵坐标为1, ∴1=﹣ ![]() ,
,
∴x=﹣3,
∵ax2+bx+ ![]() =0化为于x的方程ax2+bx=﹣
=0化为于x的方程ax2+bx=﹣ ![]() 的形式,
的形式,
∴此方程的解即为两函数图象交点的横坐标的值,
∴x=﹣3.
所以答案是:x=﹣3.
【考点精析】解答此题的关键在于理解反比例函数的图象的相关知识,掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点,以及对二次函数的图象的理解,了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,一次函数
 的图象是直线l1 , l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
的图象是直线l1 , l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位. 
(1)写出A点的坐标和AB的长;
(2)当点P、Q运动了多少秒时,以点Q为圆心,PQ为半径的⊙Q与直线l2、y轴都相切,求此时a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系XOY中,直线l1过点A(1,0)且与y轴平行,直线l2过点B(0,2)且与x轴平行,直线l1与直线l2相交于点P.点E为直线l2上一点,反比例函数
 (k>0)的图象过点E与直线l1相交于点F.
(k>0)的图象过点E与直线l1相交于点F. 
(1)若点E与点P重合,求k的值;
(2)连接OE、OF、EF.若k>2,且△OEF的面积为△PEF的面积的2倍,求E点的坐标;
(3)是否存在点E及y轴上的点M,使得以点M、E、F为顶点的三角形与△PEF全等?若存在,求E点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )

A.30,2
B.60,2
C.60,
D.60,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,立方体的六个面上标着连续的整数,若相对的两个面上所标之数的和相等.则这六个数的和为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)|﹣ |﹣(﹣2011)0+4÷(﹣2)3
|﹣(﹣2011)0+4÷(﹣2)3
(2)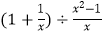 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并写出它的所有整数解.
,并写出它的所有整数解.
相关试题

