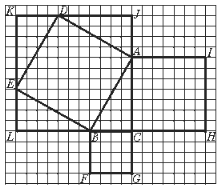
【题目】下图甲是任意一个直角三角形ABC,它的两条直角边的边长分别为a、b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.
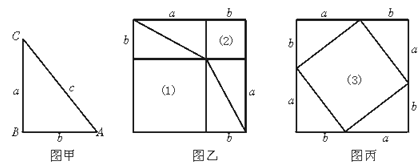
①图乙和图丙中(1)(2)(3)是否为正方形?为什么?
②图中(1)(2)(3)的面积分别是多少?
③图中(1)(2)的面积之和是多少?
④图中(1)(2)的面积之和与正方形(3)的面积有什么关系?为什么?
由此你能得到关于直角三角形三边长的关系吗?

参考答案:
【答案】见解析
【解析】
试题根据正方形的面积公式依次分析即可.
①图乙、图丙中(1)(2)(3)都是正方形.易得(1)是以a为边长的正方形,(2)是以b为边长的正方形,(3)的四条边长都是c,且每个角都是直角,所以(3)是以c为边长的正方形.
②图中(1)的面积为a2,(2)的面积为b2,(3)的面积为c2.
③图中(1)(2)面积之和为a2+b2.
④图中(1)(2)面积之和等于(3)的面积.
因为图乙、图丙都是以a+b为边长的正方形,它们面积相等,(1)(2)的面积之和与(3)的面积都等于(a+b)2减去四个Rt△ABC的面积.
由此可得:任意直角三角形两直角边的平方和等于斜边的平方,即勾股定理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )
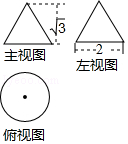
A.2π
B.4π
C.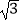 π
π
D.2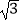 π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】在两千多年前我国古算术上记载有“勾三股四弦五”.你知道它的意思吗?
它的意思是说:如果一个直角三角形的两条直角边长分别为3和4个长度单位,那么它的斜边的长一定是5个长度单位,而且3、4、5这三个数有这样的关系:32+42=52.
(1)请你动动脑筋,能否验证这个事实呢?该如何考虑呢?
(2)请你观察下列图形,直角三角形ABC的两条直角边的长分别为AC=7,BC=4,请你研究这个直角三角形的斜边AB的长的平方是否等于42+72?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB=AC,且AB⊥AC,D在BC上,求证:
 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价) 甲
乙
进价(元/件)
20
30
售价(元/件)
29
40
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
-
科目: 来源: 题型:
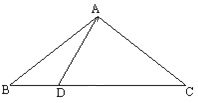
查看答案和解析>>【题目】已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A。
求:BD的长。
相关试题

