【题目】在两千多年前我国古算术上记载有“勾三股四弦五”.你知道它的意思吗?
它的意思是说:如果一个直角三角形的两条直角边长分别为3和4个长度单位,那么它的斜边的长一定是5个长度单位,而且3、4、5这三个数有这样的关系:32+42=52.
(1)请你动动脑筋,能否验证这个事实呢?该如何考虑呢?
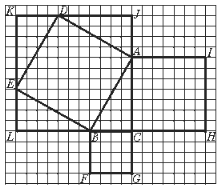
(2)请你观察下列图形,直角三角形ABC的两条直角边的长分别为AC=7,BC=4,请你研究这个直角三角形的斜边AB的长的平方是否等于42+72?
参考答案:
【答案】见解析
【解析】
(1)边长的平方即以此边长为边的正方形的面积,故可通过面积验证.分别以这个直角三角形的三边为边向外做正方形,求出三个正方形的面积,即可证明;
(2)关键是计算S正方形ABED=S正方形KLCJ﹣4SRt△ABC,再加以验证即可.
(1)边长的平方即以此边长为边的正方形的面积,故可通过面积验证.分别以这个直角三角形的三边为边向外作正方形,如图:AC=4,BC=3,

S正方形ABED=S正方形FCGH﹣4SRt△ABC
=(3+4)2﹣4×![]() ×3×4
×3×4
=72﹣24
=25,
即AB2=25,
又∵AC=4,BC=3,
AC2+BC2=42+32=25
∴AB2=AC2+BC2.
(2)如图

S正方形ABED=S正方形KLCJ﹣4SRt△ABC=(4+7)2﹣4×![]() ×4×7=121﹣56=65=42+72.
×4×7=121﹣56=65=42+72.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC中,∠C=90°.
(1)若a=5,b=12,则c=________;
(2)若a=6,c=10,则b=_______;
(3)若a∶b=3∶4,c=10,则a=_______,b=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】折叠矩形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
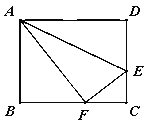
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )
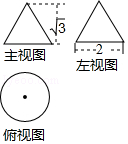
A.2π
B.4π
C.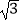 π
π
D.2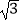 π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下图甲是任意一个直角三角形ABC,它的两条直角边的边长分别为a、b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.
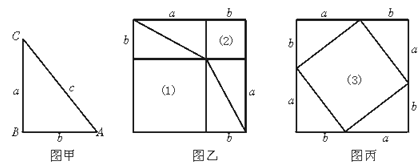
①图乙和图丙中(1)(2)(3)是否为正方形?为什么?
②图中(1)(2)(3)的面积分别是多少?
③图中(1)(2)的面积之和是多少?
④图中(1)(2)的面积之和与正方形(3)的面积有什么关系?为什么?
由此你能得到关于直角三角形三边长的关系吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB=AC,且AB⊥AC,D在BC上,求证:
 。
。
相关试题

