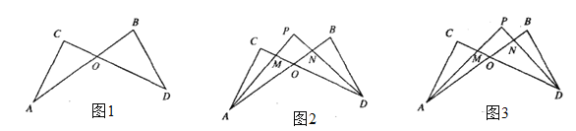
【题目】如图1，线段AB、CD相交于点O，连结AC、BD，我们把形如图1的图形称之为“8字形”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥聪明才智，解决以下问题：

(1)在图1中，请写出∠A、∠B、∠C、∠D之间的数量关系，并说明理由；

(2)仔细观察，在图2中“8字形”的个数有 个；

(3)在图2中，若∠B＝70°，∠C＝84°，∠CAB和∠BDC的平分线AP和DP相交于点P，并且与CD、AB分别相交于M、N利用(1)的结论，试求∠P的度数；

(4)在图3中，如果∠B和∠C为任意角，并且AP和DP分别是∠CAB和∠BDC的四等分线，即∠PAO＝∠CAO， ∠BDP＝∠BDO，那么∠P与∠C、∠B之间存在的数量关系是 （直接写出结论即可）．

参考答案：

【答案】（1）∠A+∠C=∠D+∠B；（2）6；（3）77°；（4）

【解析】

（1）根据三角形的内角和即可得到结论；
（2）以线段AC为边的“8字型”有3个，以点O为交点的“8字型”有4个；
（3）根据角平分线的定义得到∠CAP=∠BAP，∠BDP=∠CDP，再根据三角形内角和定理得到∠CAP+∠C=∠CDP+∠P，∠BAP+∠P=∠BDP+∠B，两等式相减得到∠C-∠P=∠P-∠B，即∠P=（∠C+∠B），然后把∠B＝70°，∠C＝84°代入计算即可；

（4）同（3）的步骤可求出∠P与∠C、∠B之间存在的数量关系.

（1）∠A+∠C=∠D+∠B，

∵∠A+∠C+∠AOC=∠D+∠B+∠BOD=180°,

∠AOC=∠BOD,

∴∠A+∠C=∠D+∠B；

（2）交点有点M、N各有1个，交点O有4个，所以，“8字形”图形共有6个；

（3）∵∠CAB和∠BDC的平分线AP和DP相交于点P，

∴∠CAP=∠BAP，∠BDP=∠CDP，

∵∠CAP+∠C=∠CDP+∠P，∠BAP+∠P=∠BDP+∠B，

∴∠C-∠P=∠P-∠B，

即∠P=（∠C+∠B），

∵∠C=84°，∠B=70°

∴∠P=（∠C+∠B）=（84°+70°）=77°.

(4) ∵∠PAO＝∠CAO， ∠BDP＝∠BDO，

∴∠PAC＝∠CAO， ∠ODP＝∠BDO，

∵∠CAP+∠C=∠ODP+∠P，∠BAP+∠P=∠BDP+∠B，

∴∠CAO +∠C=∠BDO +∠P，∠CAO +∠P=∠BDO +∠B，

∴∠CAO +3∠P=∠BDO +3∠B，

∴∠C-3∠P=∠P-3∠B，

∴ .

关闭