【题目】如图,已知数轴上点A表示的数为-3,B是数轴上位于点A右侧一点,且AB=12.动点P从点A出发,以每秒2个单位长度的速度沿数轴向点B方向匀速运动,设运动时间为t秒.
(1)数轴上点B表示的数为______;点P表示的数为______(用含t的代数式表示).
(2)动点Q从点B出发,以每秒1个单位长度的速度沿数轴向点A方向匀速运动;点P、点Q同时出发,当点P与点Q重合后,点P马上改变方向,与点Q继续向点A方向匀速运动(点P、点Q在运动过程中,速度始终保持不变);当点P到达A点时,P、Q停止运动.设运动时间为t秒.
①当点P与点Q重合时,求t的值,并求出此时点P表示的数.
②当点P是线段AQ的三等分点时,求t的值.
![]()
参考答案:
【答案】(1)9, -3+2t;(2)①当t=4时,点P与点Q重合,此时点P表示的数为5;②当t=![]() 秒或3秒或6秒或
秒或3秒或6秒或![]() 秒时,点P是线段AQ的三等分点.
秒时,点P是线段AQ的三等分点.
【解析】
(1)根据两点间的距离求解可得;
(2)①根据重合前两者的路程和等于AB的长度列方程求解可得;②分点P与点Q重合前和重合后,依据点P是线段AQ的三等分点线段间的数量关系,并据此列出方程求解可得.
解:(1)由题意知,点B表示的数是-3+12=9,点P表示的数是-3+2t,
故答案为:9,-3+2t;
(2)①根据题意,得:(1+2)t=12,
解得:t=4,
∴-3+2t=-3+2×4=5,
答:当t=4时,点P与点Q重合,此时点P表示的数为5;
②P与Q重合前:
当2AP=PQ时,有2t+4t+t=12,解得t=![]() ;
;
当AP=2PQ时,有2t+t+t=12,解得t=3;
P与Q重合后:
当AP=2PQ时,有2(8-t)=2(t-4),解得t=6;
当2AP=PQ时,有4(8-t)=t-4,解得t=![]() ;
;
综上所述,当t=![]() 秒或3秒或6秒或
秒或3秒或6秒或![]() 秒时,点P是线段AQ的三等分点.
秒时,点P是线段AQ的三等分点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,线段AB、CD相交于点O,连结AC、BD,我们把形如图1的图形称之为“8字形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥聪明才智,解决以下问题:
(1)在图1中,请写出∠A、∠B、∠C、∠D之间的数量关系,并说明理由;
(2)仔细观察,在图2中“8字形”的个数有 个;
(3)在图2中,若∠B=70°,∠C=84°,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N利用(1)的结论,试求∠P的度数;
(4)在图3中,如果∠B和∠C为任意角,并且AP和DP分别是∠CAB和∠BDC的四等分线,即∠PAO=
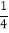 ∠CAO, ∠BDP=
∠CAO, ∠BDP= ∠BDO,那么∠P与∠C、∠B之间存在的数量关系是 (直接写出结论即可).
∠BDO,那么∠P与∠C、∠B之间存在的数量关系是 (直接写出结论即可).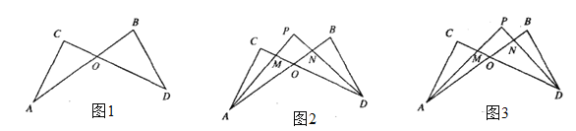
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB,点C、点D在直线AB上,并且CD=8,AC:CB=1:2,BD:AB=2:3,则AB=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”是一样的,后面的就改用手势了.下面两个图框是用法国“小九九”计算7×8和8×9的两个示例.若用法国的“小九九”计算7×9,左、右手依次伸出手指的个数是( )


A. 2,3B. 3,3C. 2,4D. 3,4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)平面内将一副三角板按如图1所示摆放,∠EBC= °;
(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α= °;
(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是直线AC上一点,EF是∠AEB的平分线.
(1)如图1,若EG是∠BEC的平分线,求∠GEF的度数;
(2)如图2,若GE在∠BEC内,且∠CEG=3∠BEG,∠GEF=75°,求∠BEG的度数.
(3)如图3,若GE在∠BEC内,且∠CEG=n∠BEG,∠GEF=α,求∠BEG(用含n、α的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】【操作发现】
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.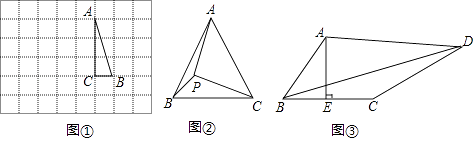
(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B= .
(3)【问题解决】
如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
(4)【灵活运用】
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示).
相关试题

