【题目】如图,在半径为 ![]() 的
的 ![]() 中,弦
中,弦 ![]() ,
,![]() 是弦
是弦 ![]() 所对的优弧上的动点,连接
所对的优弧上的动点,连接 ![]() , 过点
, 过点 ![]() 作
作 ![]() 的垂线交射线
的垂线交射线 ![]() 于点
于点 ![]() ,当
,当 ![]() 是等腰三角形时,线段
是等腰三角形时,线段 ![]() 的长为____.
的长为____.

参考答案:
【答案】![]() 或8或
或8或![]()
【解析】试题分析:①当BA=BP时,
易得AB=BP=BC=8,即线段BC的长为8.
②当AB=AP时,如图1,延长AO交PB于点D,过点O作OE⊥AB于点E,则AD⊥PB,AE=![]() AB=4,
AB=4,
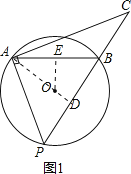
∴BD=DP,
在Rt△AEO中,AE=4,AO=5,
∴OE=3,
易得△AOE∽△ABD,
∴![]() ,
,
∴BD=![]() ,
,
∴BD=PD=![]() ,即PB=
,即PB=![]() ,
,
∵AB=AP=8,
∴∠ABD=∠P,
∵∠PAC=∠ADB=90°,
∴△ABD∽△CPA,
∴![]() ,
,
∴CP=![]() ,
,
∴BC=CP-BP=![]()
![]() =
=![]() ;
;
③当PA=PB时
如图2,连接PO并延长,交AB于点F,过点C作CG⊥AB,交AB的延长线于点G,连接OB,
则PF⊥AB,
∴AF=FB=4,
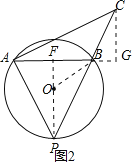
在Rt△OFB中,OB=5,FB=4,
∴OF=3,
∴FP=8,
易得△PFB∽△CGB,
∴![]() ,
,
设BG=t,则CG=2t,
易得∠PAF=∠ACG,
∵∠AFP=∠AGC=90°,
∴△APF∽△CAG,
∴![]() ,
,
∴![]() ,
,
解得t![]() ,
,
在Rt△BCG中,BC=![]() t=
t=![]() ,
,
综上所述,当△PAB是等腰三角形时,线段BC的长为8,![]() ,
,![]() ,
,
故答案为:8,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
(1)求A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));正方形A2B2C2D2的面积为________,以此下去…,则正方形AnBnCnDn的面积为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空,如图:方格纸中每个小正方形的边长都为 1,
 的顶点都在方格纸的格点上,
的顶点都在方格纸的格点上,将
 经过一次平移后得到
经过一次平移后得到 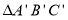 .图中标 出了点
.图中标 出了点  的对应点
的对应点  .
.(1)请画出平移后的
 ;
;(2)若连接
 ,
,  ,则这两条线段的关系是_____;
,则这两条线段的关系是_____;(3)利用网格画出
 中
中  边上的中线
边上的中线  以及
以及 边上的高
边上的高  ;
;(4)线段
 在平移过程中扫过区域的面积为 _____.
在平移过程中扫过区域的面积为 _____.
相关试题

