【题目】画图并填空,如图:方格纸中每个小正方形的边长都为 1,![]() 的顶点都在方格纸的格点上,
的顶点都在方格纸的格点上,
将 ![]() 经过一次平移后得到
经过一次平移后得到 ![]() .图中标 出了点
.图中标 出了点 ![]() 的对应点
的对应点 ![]() .
.
(1)请画出平移后的![]() ;
;
(2)若连接 ![]() ,
, ![]() ,则这两条线段的关系是_____;
,则这两条线段的关系是_____;
(3)利用网格画出 ![]() 中
中 ![]() 边上的中线
边上的中线 ![]() 以及
以及![]() 边上的高
边上的高 ![]() ;
;
(4)线段 ![]() 在平移过程中扫过区域的面积为 _____.
在平移过程中扫过区域的面积为 _____.

参考答案:
【答案】(1)见解析;(2)平行且相等;(3)见解析;(4)20
【解析】
(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用平移的性质得出两条线段之间的关系;
(3)利用网格得出AC的中点即可得出答案;利用网格得出高CE即可得出答案;
(4)直接线段AB在平移过程中扫过区域的面积进而得出答案.
解:(1)如图所示,
(2)根据平移的性质可得,AA′∥BB′,AA′=BB′,
故答案为:平行且相等;
(3)如图所示;
(4)线段AB在平移过程中扫过区域的面积=S四边形AA′B′B=5×4=20.
故答案为:20.
故答案为:(1)见解析;(2)平行且相等;(3)见解析;(4)20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为
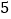 的
的 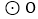 中,弦
中,弦 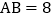 ,
,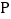 是弦
是弦 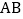 所对的优弧上的动点,连接
所对的优弧上的动点,连接  , 过点
, 过点 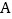 作
作  的垂线交射线
的垂线交射线 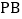 于点
于点 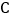 ,当
,当 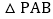 是等腰三角形时,线段
是等腰三角形时,线段 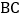 的长为____.
的长为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
(1)求A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));正方形A2B2C2D2的面积为________,以此下去…,则正方形AnBnCnDn的面积为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数。
例如,
 展开式中的系数1、2、1恰好对应图中第三行的数字;
展开式中的系数1、2、1恰好对应图中第三行的数字;再如,
 展开式中的系数1、3、3、1恰好对应图中第四行的数字。
展开式中的系数1、3、3、1恰好对应图中第四行的数字。请认真观察此图,写出(a+b)4的展开式,(a+b)4=_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径为
 ,点
,点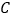 在圆周上(异于
在圆周上(异于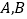 ),
),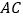 是
是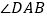 的平分线,
的平分线,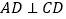 .
.(1)求证:直线
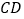 是⊙O的切线;
是⊙O的切线;(2)若
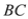 =3,
=3,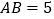 ,求
,求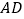 的值.
的值.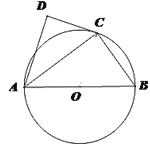
相关试题

