【题目】证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等,已知:
如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴ = ( ).
同理可得,PB= .
∴ = (等量代换).
∴ (到一条线段两个端点距离相等的点,在这条线段的 )
∴AB、BC、AC的垂直平分线 .
参考答案:
【答案】PB;PA;垂直平分线上任意一点,到线段两端点的距离相等;PC;垂直平分线上任意一点,到线段两端点的距离相等;PA;PC;点P是AC边垂直平线上的一点;垂直平分线上;相交于点P.
【解析】
试题分析:根据线段垂直平分线的性质可得出PB=PA,同理可得出PA=PC,由此即可得出PA=PC,再根据线段垂直平分线的性质可得出点P是AC边垂直平线上的一点,从而证出结论.
证明:∵点P是AB边垂直平线上的一点,
∴PB=PA (垂直平分线上任意一点,到线段两端点的距离相等).
同理可得,PB=PC(垂直平分线上任意一点,到线段两端点的距离相等).
∴PA=PC(等量代换).
∴点P是AC边垂直平线上的一点(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),
∴AB、BC、AC的垂直平分线相交于点P.
故答案为:PB;PA;垂直平分线上任意一点,到线段两端点的距离相等;PC;垂直平分线上任意一点,到线段两端点的距离相等;PA;PC;点P是AC边垂直平线上的一点;垂直平分线上;相交于点P.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为
 ;④
;④ ,其中所有正确结论的序号是 .
,其中所有正确结论的序号是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】多边形剪掉一个角后的内角和为1260°.则该多边形剪之前的边数不可能是( )
A.七B.八C.九D.十
-
科目: 来源: 题型:
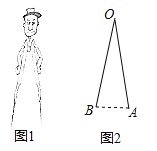
查看答案和解析>>【题目】如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.
(1)当∠AOB=18°时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到0.01cm)
(参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科学计算器)
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式:①16x2﹣8x;②(x﹣1)2﹣4(x﹣1)+4;③(x+1)4﹣4x(x+1)2+4x2;④﹣4x2﹣1+4x 分解因式后,结果中含有相同因式的是( )
A.①和②B.③和④C.①和④D.②和③
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式(a+b)2-4(a2-b2)+4(a-b)2因式分解的结果为( )
A.(3a-b)2
B.(3b+a)2
C.(3b-a)2
D.(3a+b)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(2m+4,3m+3)在x轴上,则点P的坐标为
相关试题

