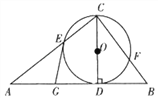
【题目】如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA, CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.
参考答案:
【答案】证明见解析
【解析】试题分析: (证法一): 连接OE,DE根据已知条件可证得∠1=∠2,∠3=∠4,再由∴∠1+∠3=∠2+∠4 ,即可证得∠OEG=∠ODG=90°,结论得证;(证法二):连接OE,OG,证得OG∥AC,根据平行线的性质可得∠1=∠2,∠3=∠4,根据等腰三角形的的性质可得∠2=∠4,即可得∠1=∠3,利用SAS证得△OEG≌△ODG,即可得∠OEG=∠ODG=90°,结论得证.
试题解析:
(证法一)
证明:连接OE,DE ,
∵CD是⊙O的直径,
∴∠AED=∠CED=90°,
∵G是AD的中点,
∴EG=![]() AD=DG,∴∠1=∠2;
AD=DG,∴∠1=∠2;
∵OE=OD,∴∠3=∠4 ,
∴∠1+∠3=∠2+∠4 ,
∴∠OEG=∠ODG=90°,
故GE是⊙O的切线。
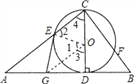
(证法二)
证明:连接OE,OG,
∵AG=GD,CO=OD,
∴OG∥AC ,
∴∠1=∠2,∠3=∠4.
∵OC=OE,∴∠2=∠4,
∴∠1=∠3 ,
又OE=OD,OG=OG,
∴△OEG≌△ODG,
∴∠OEG=∠ODG=90°,
∴GE是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB∥CD,AD∥BC,OE=OF,则图中全等三角形的组数是( )

A.3组B.4组C.5组D.6组
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.
(1)求C点坐标;
(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.
(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
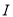 为
为 角平分线交点,
角平分线交点, 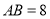 ,
,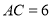 ,
,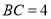 ,将
,将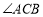 平移使其顶点
平移使其顶点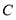 与
与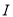 重合,则图中阴影部分的周长为( )
重合,则图中阴影部分的周长为( )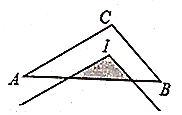
A.
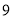 B.
B. 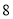 C.
C. 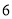 D.
D. 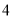
-
科目: 来源: 题型:
查看答案和解析>>【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为
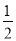 .
.(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
-
科目: 来源: 题型:
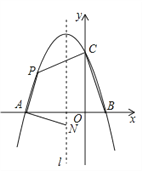
查看答案和解析>>【题目】如图,抛物线
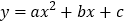
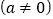 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴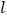 为
为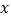 =–1,P为抛物线上第二象限的一个动点.
=–1,P为抛物线上第二象限的一个动点.(1)求抛物线的解析式并写出其顶点坐标;
(2)当点P的纵坐标为2时,求点P的横坐标;
(3)当点P在运动过程中,求四边形PABC面积最大时的值及此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画抛物线y=x2﹣2x﹣3的草图,并说出开口方向,对称轴,顶点坐标,增减性,最值.
相关试题

