【题目】画抛物线y=x2﹣2x﹣3的草图,并说出开口方向,对称轴,顶点坐标,增减性,最值.
参考答案:
【答案】见解析
【解析】试题分析:
(1)画二次函数图象,至少要描出5个点,其中顶点坐标必取,与坐标轴的交点,如果有,建议取,所取点,尽量在对称轴两边对称选取,否则图象不对称不完整.
(2)a大小决定开口方向,而a=1>0,故开口向上;对称轴为直线![]() ,顶点为
,顶点为![]() 即(1,-4); 令x=0,则y=-3,得与y轴交点(0,-3);令y=0,得方程x2﹣2x﹣3=0,解之得
即(1,-4); 令x=0,则y=-3,得与y轴交点(0,-3);令y=0,得方程x2﹣2x﹣3=0,解之得![]() ,得与x轴两个交点(3,0),(-1,0).
,得与x轴两个交点(3,0),(-1,0).
(3)列表后描点,然后用平滑曲线连接各点,就得所求作的图象.
(4)根据草图,增减性,最值就一目了然.
解:列表,如下:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
描点、连线,如图所示.
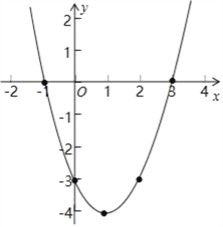
观察函数图象,可知:抛物线开口向上;对称轴为直线x=1;顶点坐标为(1,﹣4);当x<1时,y随x增大而减小,当x>1时,y随x增大而增大;抛物线y=x2﹣2x﹣3存在最小值,最小值为﹣4.
-
科目: 来源: 题型:
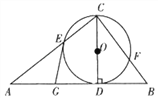
查看答案和解析>>【题目】如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA, CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为
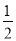 .
.(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
-
科目: 来源: 题型:
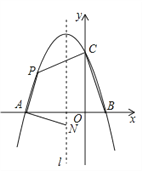
查看答案和解析>>【题目】如图,抛物线
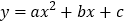
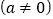 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴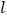 为
为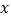 =–1,P为抛物线上第二象限的一个动点.
=–1,P为抛物线上第二象限的一个动点.(1)求抛物线的解析式并写出其顶点坐标;
(2)当点P的纵坐标为2时,求点P的横坐标;
(3)当点P在运动过程中,求四边形PABC面积最大时的值及此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
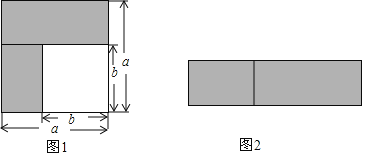
小题1:如图1,可以求出阴影部分的面积是_______ (写成两数平方差的形式);
小题2:如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_______,长是______,面积是_________ (写成多项式乘法的形式).
小题3:比较图 1,图2的阴影部分面积,可以得到乘法公式________ (用式子表达).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2(a≠0)与一次函数y=kx﹣2的图象相交于A、B两点,如图所示,其中A(﹣1,﹣1),求△OAB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,设甲、乙、丙、丁分别表示△ABC,△ACD,△EFG,△EGH.已知∠ACB=∠CAD=∠EFG=∠EGH=70°,∠BAC=∠ACD=∠EGF=∠EHG=50°,则叙述正确的是( )
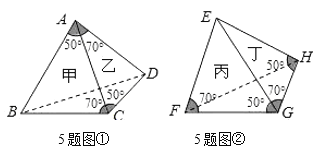
A.甲、乙全等,丙、丁全等B.甲、乙全等,丙、丁不全等
C.甲、乙不全等,丙、丁全等D.甲、乙不全等,丙、丁不全等
相关试题

