【题目】已知抛物线![]()
(1)写出该抛物线的顶点D坐标和对称轴.
(2)抛物线与![]() 轴交于A,B两点,求△ABD的面积
轴交于A,B两点,求△ABD的面积

参考答案:
【答案】(1)(-1,4),直线![]() = -1(2)8
= -1(2)8
【解析】(1)将二次函数配方后即可求得其顶点坐标及对称轴;
(2)根据上题确定的二次函数的顶点坐标和抛物线与坐标轴的交点坐标就能够求得△ABD的面积.
解:(1)由y=-x2-2x+3= -( x2+2x-3)=-( x2+2x+1-3-1)= -(x+1)2+4,
∴该抛物线的顶点D坐标为(-1,4)对称轴x=-1,
(2)令y=0,-x2-2x+3=0,则x2+2x-3=0,
(x+3)(x-1)=0,x1=-3,x2=1,
∴A(-3,0),B(1,0).
又∵D(-1,4),
∴AB=4,OC=4,
∴S△ABC=![]() AB×OC=
AB×OC=![]() ×4×4=8.
×4×4=8.
“点睛”本题考查了二次函数的性质,解题的关键是能够利用配方法确定二次函数的顶点坐标和抛物线与坐标轴的交点坐标,难度不大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种商品每件成本a元,原来按成本增加25%定出价格,现在由于库存积压减价,按原价的90%出售,现售价多少元?每件还能盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为一个平行四边形ABCD,其中H、G两点分别在BC、CD上,AH⊥BC,AG⊥CD,且AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4四个角.若AH=5,AG=6,则下列关系何者正确( )

A.∠1=∠2
B.∠3=∠4
C.BH=GD
D.HC=CG -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线
 与
与 轴交于A,B(点A在点B的右边),与
轴交于A,B(点A在点B的右边),与 轴交于点C.过A,C两点作直线
轴交于点C.过A,C两点作直线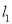 ,P是抛物线上的动点,过P作PD⊥
,P是抛物线上的动点,过P作PD⊥ 轴,垂足为D,交直线
轴,垂足为D,交直线 于点E.设点P的横坐标为
于点E.设点P的横坐标为 .
.(1)求直线
 的函数表达式;
的函数表达式;(2)问是否存在点P,使O,E,C,P四点能构成平行四边形,若存在,请求出
 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)如图2,过A点作直线
 ⊥
⊥ ,连接OE,作△AOE的外接圆,交直线
,连接OE,作△AOE的外接圆,交直线 于点F,连接OF,EF.当△EOF的面积最小时,求点P的坐标和最小值.
于点F,连接OF,EF.当△EOF的面积最小时,求点P的坐标和最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】长度为1㎝、2㎝、3㎝、4㎝、5㎝的五条线段,若以其中的三条线段为边构成三角形,可以构成不同的三角形共有( )
A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形ABC中,若AB=16cm,AC=12cm,BC=20cm.点P从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,如果点P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,请用含t的代数式表示,①当点Q在AC上时,CQ= ;②当点Q在AB上时,AQ= ;
③当点P在AB上时,BP= ;④当点P在BC上时,BP= .
(2)如图2,若点P在线段AB上运动,点Q在线段CA上运动,当QA=AP时,试求出t的值.
(3)如图3,当P点到达C点时,P、Q两点都停止运动,当AQ=BP时,试求出t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】圆柱形纸筒沿母线AB剪开铺平,得到一个矩形(如图).如果将这个纸筒沿线路BMA剪开铺平,得到的图形是( )
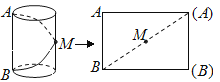
A.矩形
B.半圆
C.三角形
D.平行四边形
相关试题

