【题目】圆柱形纸筒沿母线AB剪开铺平，得到一个矩形（如图）．如果将这个纸筒沿线路BMA剪开铺平，得到的图形是（　　）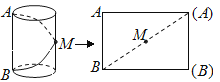
A.矩形
B.半圆
C.三角形
D.平行四边形

参考答案：

【答案】D
【解析】严格按照图中的方法亲自动手操作一下，即可很直观地呈现出来．
M是所在母线的中点，如果将这个纸筒沿线路BMA剪开，即把圆柱延AB与M所在母线平方在一个平面内，再剪开AM，BM．则得到两个重合的△ABM，△ABM是等腰三角形，且AB是底边，展开后得到的图形是一个以△ABM的腰AM、BM为边的四边形，相对的边对应相等，所以是平行四边形．
故选D．
【考点精析】通过灵活运用平行四边形的判定，掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形即可以解答此题．

关闭