【题目】如图所示,在菱形ABCD中,∠BAD=120°,AB=4.求: 
(1)对角线AC,BD的长;
(2)菱形ABCD的面积.
参考答案:
【答案】
(1)解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAD=120°,
∴∠BAC=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∵四边形ABCD是菱形,
∴AC⊥BD,A0=2,
∴OD= ![]() =
= ![]() =2
=2 ![]() ,
,
∴BD=4 ![]()
(2)解:面积为 ![]() AC×BD=
AC×BD= ![]() =8
=8 ![]()
【解析】(1)根据菱形的性质可得AB=BC,然后再证明△ABC是等边三角形,从而可得AC=AB=4,进而可得AO=2,再利用勾股定理计算BO长,进而可得BD长;(2)利用菱形的面积= ![]() ab(a、b是两条对角线的长度)可得面积.
ab(a、b是两条对角线的长度)可得面积.
【考点精析】利用菱形的性质对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
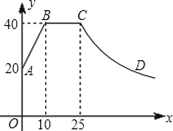
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲16分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根,则m的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的5×5的正方形网格中,每个小正方形的边长均为1,按下列要求画图或填空;
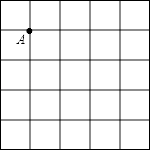
(1)画一条线段AB使它的另一端点B落在格点上(即小正方形的顶点),且AB=2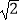 ;
;
(2)以(1)中的AB为边画一个等腰△ABC,使点C落在格点上,且另两边的长都是无理数;
(3)△ABC的周长为 , 面积为 . -
科目: 来源: 题型:
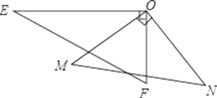
查看答案和解析>>【题目】如图,一副三角板的两个直角顶点重合在一起.
(1)若∠EON=110°,求∠MOF的度数;
(2)比较∠EOM与∠FON的大小,并写出理由;
(3)求∠EON+∠MOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3)班的50名同学进行物理、化学两种实验测试,经最后统计知:物理实验做对的有40人,化学实验做对的有31人,两种实验都做错的有4人,则这两种实验都做对的有( )
A.17人
B.21人
C.25人
D.37人 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AOB是一条直线,OC是∠AOD的平分线,OE 是∠BOD的平分线.
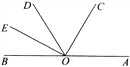
(1)若∠AOE=140°,求∠AOC的度数;
(2)若∠EOD :∠COD=2 : 3,求∠COD的度数.
相关试题

