【题目】为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
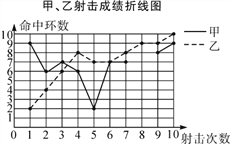
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | |||
乙 | 1 |
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁将胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
参考答案:
【答案】(1)见解析;(2)甲胜出;(3)见解析.
【解析】试题分析:(1)根据折线统计图列举出乙的成绩,计算出甲的中位数,方差,以及乙平均数,中位数及方差,补全即可;
(2)计算出甲乙两人的方差,比较大小即可做出判断;
(3)希望甲胜出,规则改为9环与10环的总数大的胜出,因为甲9环与10环的总数为4环.
试题解析:(1)如图所示.

甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | 7 | 4 | 0 |
乙 | 7 | 7.5 | 5.4 | 1 |
(2)由甲的方差小于乙的方差,甲比较稳定,故甲胜出.
(3)如果希望乙胜出,应该制定的评判规则为:平均成绩高的胜出;如果平均成绩相同,则随着比赛的进行,发挥越来越好者或命中满环(10环)次数多者胜出.因为甲、乙的平均成绩相同,随着比赛的进行,乙的射击成绩越来越好(回答合理即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O是直线AB上一点,将一直角三角尺如图QZ-13(a)放置,一直角边ON在直线AB上,另一直角边OM与AB所形成的∠AOM=90°,射线OC在∠AOM内部.
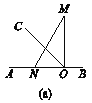

(探究)如图(b),将三角尺绕着点O顺时针旋转,当∠AON=∠CON时,试判断OM是否平分∠BOC,并说明理由.
(拓展)若∠AOC=80°时,三角尺OMN绕O点顺时针旋转一周,每秒旋转5°,则多少秒后,∠MOC=∠MOB?
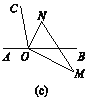
(延伸)在上述条件下,如图(c),旋转三角尺使ON在∠BOC内部,另一边OM在直线AB的另一侧,下面两个结论:①∠NOC-∠BOM的值不变;②∠NOC+∠BOM的值不变.选择其中一个正确的结论说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲、乙得分的平均数都是8 B. 甲得分的众数是8,乙得分的众数是9
C. 甲得分的中位数是9,乙得分的中位数是6 D. 甲得分的方差比乙得分的方差小
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次大学生一年级新生训练射击比赛中,某小组的成绩如表
环数
6
7
8
9
人数
1
5
3
1
(1)该小组射击数据的众数是 .
(2)该小组的平均成绩为多少?(要写出计算过程)
(3)若8环(含8环)以上为优秀射手,在1200名新生中有多少人可以评为优秀射手?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
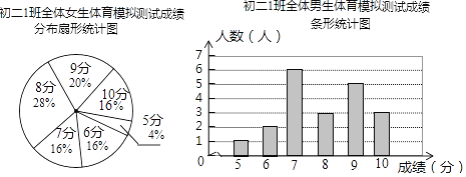
初二1班体育模拟测试成绩分析表
平均分
方差
中位数
众数
男生
2
8
7
女生
7.92
1.99
8
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表.
-
科目: 来源: 题型:
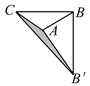
查看答案和解析>>【题目】如图,用一个平面去截一个正方体,如果截去的几何体是一个三棱锥,请回答下列问题:
(1)截面一定是什么图形?
(2)剩下的几何体可能有几个顶点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆柱的底面半径是10 cm,高是18 cm,把这个圆柱放在水平桌面上,如图所示.
(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?
(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?
(3)怎样截时所得的截面是长方形且长方形的面积最大,请你画出这个截面并求其面积.

相关试题

