【题目】在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为cm2 .
参考答案:
【答案】126或66
【解析】解:当∠B为锐角时(如图1), 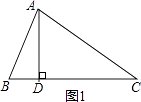
在Rt△ABD中,
BD= ![]() =
= ![]() =5cm,
=5cm,
在Rt△ADC中,
CD= ![]() =
= ![]() =16cm,
=16cm,
∴BC=21,
∴S△ABC= ![]() =
= ![]() ×21×12=126cm2;
×21×12=126cm2;
当∠B为钝角时(如图2),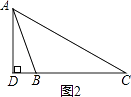
在Rt△ABD中,
BD= ![]() =
= ![]() =5cm,
=5cm,
在Rt△ADC中,
CD= ![]() =
= ![]() =16cm,
=16cm,
∴BC=CD﹣BD=16﹣5=11cm,
∴S△ABC= ![]() =
= ![]() ×11×12=66cm2 ,
×11×12=66cm2 ,
故答案为:126或66.
此题分两种情况:∠B为锐角或∠B为钝角已知AB、AC的值,利用勾股定理即可求出BC的长,利用三角形的面积公式得结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】相反数等于-5的数是( )
A.5
B.-5
C.5或-5
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】点A(0,5)关于原点对称,得到点A′,那么A′的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解抛物线
 上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.
上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.问题解决
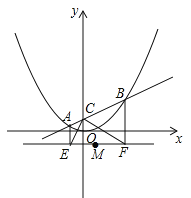
如图,在平面直角坐标系中,直线
 与y轴交于C点,与函数
与y轴交于C点,与函数 的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.
的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.(1)写出点C的坐标,并说明∠ECF=90°;
(2)在△PEF中,M为EF中点,P为动点.
①求证:
 ;
;②已知PE=PF=3,以EF为一条对角线作平行四边形CEDF,若1<PD<2,试求CP的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(k﹣1)x2﹣4x+4=0有实数根(注:此处并未说明此方程为一元二次方程,应分别考虑k=1与k≠1的情形),求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是确定性事件的是( )
A.甲、乙、丙三人随意站成一排,而甲恰好站中间
B.从含有1个次品的10个产品中,随意抽取一个产品恰好是次品
C.早晨,太阳从西方升起
D.明天早晨八点是上班高峰期,学校门前的公路上必塞
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
(2)﹣
(3) ﹣4
﹣4
(4) +(1﹣
+(1﹣  )0 .
)0 .
(5)(2 +
+  )(2
)(2  ﹣
﹣  )
)
(6) ÷
÷  +
+  ×
×  ﹣
﹣  .
.
相关试题

