【题目】如图,已知数轴上有A、B两点(点A在点B的左侧),且两点距离为12个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
![]()
(1)图中如果点A、B表示的数是互为相反数,那么点A表示的数是__________;
(2)当t=4秒时,点A与点P之间的距离是___________个长度单位;
(3)当点A表示的数是-2时,用含t的代数式表示点P表示的数;
(4)若点P到点A的距离是点P到点B的距离的2倍,请直接写出t的值.
参考答案:
【答案】(1)-6;(2)8;(3)-2+2t;(4)(4)4或12
【解析】
(1)由AB的长度结合A、B表示的数互为相反数,即可得出A,B表示的数;
(2)由AP=点P运动的时间×速度,即可得出结论;
(3)由点A表示的数,结合AP的长度,即可得出点P表示的数;
(4)设点A表示的数为a,则点B表示的数为a+12,结合点P表示的数,即可得出AP,BP的长度,由AP=2BP,即可得出关于x的含绝对值符号的一元一次方程,解之即可得出结论.
解:(1)∵A、B两点间的距离为12个单位长度,且A、B表示的数是互为相反数,点A在点B的左侧,
∴点A表示的数是-6,点B表示的数是6;
(2)AP=2t=2×4=8;
(3)∵点A表示的数为-2,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,
∴AP=2t,
∴点P表示的数为2t-2.
(4)设点A表示的数为a,则点B表示的数为a+12,
∴当运动时间为t秒时,点P表示的数为a+2t,
∴AP=2t,BP=|(a+12)-(a+2t)|=|12-2t|.
∵AP=2BP,
∴2t=2|12-2t|,即2t=24-4t或2t=4t-24,
解得:t=4或t=12.
∴当点P到点A的距离是点P到点B的距离的2倍时,t的值为4或12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块矩形纸片ABCD,AB=8,AD=6.将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则CF的长为________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF.求证:(1)△ADE≌△CDF;(2)∠BEF=∠BFE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】探索代数式
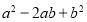 与代数式
与代数式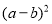 的关系.
的关系.(1)当
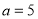 ,
,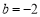 时,分别计算两个代数式的值.
时,分别计算两个代数式的值.(2)当
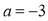 ,
,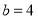 时,分别计算两个代数式的值.
时,分别计算两个代数式的值.(3)你发现了什么规律?
(4)利用你发现的规律计算:20182-2×2018×2019+20192.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(﹣
 ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
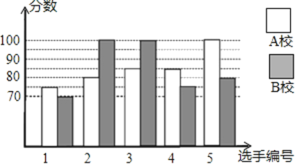
(1)根据图示填写下表:

(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,樱桃价格z(单位:元/千克)与上市时间x(单位:天)的函数关系式如图2所示.

(1)观察图象,直接写出日销售量的最大值;
(2)求小明家樱桃的日销售量y与上市时间x的函数解析式;
(3)试比较第10天与第12天的销售金额哪天多?
相关试题

