【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述4个判断中,正确的是( )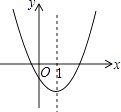
A.①②
B.①④
C.①③④
D.②③④
参考答案:
【答案】B
【解析】解:①∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴b2>4ac,故①正确;
②x=﹣2时,y=4a﹣2b+c,而题中条件不能判断此时y的正负,即4a﹣2b+c可能大于0,可能等于0,也可能小于0,故②错误;
③如果设ax2+bx+c=0的两根为α、β(α<β),那么根据图象可知不等式ax2+bx+c>0的解集是x<α或x>β,故③错误;
④∵二次函数y=ax2+bx+c的对称轴是直线x=1,
∴x=﹣2与x=4时的函数值相等,
∵4<5,
∴当抛物线开口向上时,在对称轴的右边,y随x的增大而增大,
∴y1<y2 , 故④正确.
故选:B.
【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
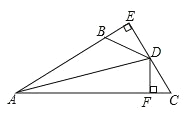
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE,点E在BC上.过点D作DF∥BC,连接DB.

求证:(1)△ABD≌△ACE;
(2)DF=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在△ABC的外部,点D边BC上,DE交AC于点F,若∠1=∠2,AE=AC,BC=DE.
(1)求证:AB=AD;
(2)若∠1=60°,判断△ABD的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=0.32,b=﹣3﹣2,c=
 ,d=
,d= ,则它们的大小关系是( )
,则它们的大小关系是( )A. a<b<c<d B. b<a<d<c C. a<d<c<b D. c<a<d<b
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两种型号的机器加工同一种零件,已知A型机器比B型机器每小时多加工20个零件,A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同.A型机器每小时加工零件的个数_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
 ,其中x的值从不等式组
,其中x的值从不等式组 的整数解中选取.
的整数解中选取.
相关试题

