【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE,点E在BC上.过点D作DF∥BC,连接DB.

求证:(1)△ABD≌△ACE;
(2)DF=CE.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)求出∠BAD=∠BAC,根据SAS证出△BAD≌△CAE即可;
(2)根据全等推出∠DBA=∠C,根据等腰三角形性质得出∠C=∠ABC,根据平行线性质得出∠ABC=∠DFB,推出∠DFB=∠DBF,根据等腰三角形的判定推出即可.
(1)∵∠BAC=∠DAE,∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,∴∠BAD=∠EAC.在△BAD和△CAE中,∵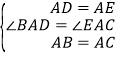 ,∴△BAD≌△CAE(SAS);
,∴△BAD≌△CAE(SAS);
(2)∵△BAD≌△CAE,∴∠DBA=∠C.
∵AB=AC,∴∠C=∠ABC.
∵DF∥BC,∴∠DFB=∠ABC=∠C=∠DBA,即∠DFB=∠DBF,∴DF=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

-
科目: 来源: 题型:
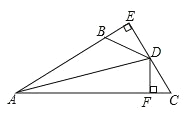
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在△ABC的外部,点D边BC上,DE交AC于点F,若∠1=∠2,AE=AC,BC=DE.
(1)求证:AB=AD;
(2)若∠1=60°,判断△ABD的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述4个判断中,正确的是( )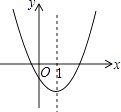
A.①②
B.①④
C.①③④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】若a=0.32,b=﹣3﹣2,c=
 ,d=
,d= ,则它们的大小关系是( )
,则它们的大小关系是( )A. a<b<c<d B. b<a<d<c C. a<d<c<b D. c<a<d<b
相关试题

