【题目】某公司有某种海产品2104千克,寻求合适价格,进行8天试销,情况如下:
第几天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
销售价格(元/千克) | 400 | A | 250 | 240 | 200 | 150 | 125 | 120 |
销售量(千克) | 30 | 40 | 48 | B | 60 | 80 | 96 | 100 |
观察表中数据,发现可以用某种函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系. 现假设这批海产品的销售中,每天销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1)猜想函数关系式: . (不必写出自变量的取值)并写出表格中A= ,B= ;
(2)试销8天后,公司决定将售价定为150元/千克. 则余下海产品预计 天可全部售出;
(3)按(2)中价格继续销售15天后,公司发现剩余海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新价格销售,那么新确定的价格最高不超过多少元/千克才能完成销售任务?
参考答案:
【答案】(1)y=![]() ,A=300,B=50;(2)余下的这些海产品预计再用20天可以全部售出;(3)新确定的价格最高不超过60元/千克才能完成销售任务.
,A=300,B=50;(2)余下的这些海产品预计再用20天可以全部售出;(3)新确定的价格最高不超过60元/千克才能完成销售任务.
【解析】
(1)根据图中数据求出反比例函数,再分别将y=40和x=240代入求出相对应的x和y;
(2)先求出8天销售的总量和剩下的数量m,将x=150代入反比例函数中得到一天的销售量y,![]() 即为所需要的天数;
即为所需要的天数;
(3)求出销售15天后剩余的数量除2得到后两天每天的销售量y,将y的值代入反比例函数中即可求出x.
(1)∵xy=12000,函数解析式为y=![]() ,
,
将y=40和x=240代入上式中求出相对应的x=300和y=50,
∴A=300,B=50;
(2)销售8天后剩下的数量m=2104-(30+40+48+50+60+80+96+100)=1600(千克),
当x=150时,y=![]() =80.
=80.
∴![]() =1600÷80=20(天),
=1600÷80=20(天),
∴余下的这些海产品预计再用20天可以全部售出;
(3)1600-80×15=400(千克),400÷2=200(千克/天),
即如果正好用2天售完,那么每天需要售出200千克.
当y=200时,x=![]() =60.
=60.
所以新确定的价格最高不超过60元/千克才能完成销售任务.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师在黑板上写了一道题:如图1,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,试比较AC+BD与AB的大小.小聪思考片刻就想出来了,他说将AB平移到CE位置,如图2,连接BE,DE,就可以比较AC+BD与AB的大小了,你知道他是怎样比较的吗?
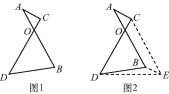
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC绕点A逆时针方向旋转得到△ADE,其中∠B=50°,∠C=60°.
(1)若AD平分∠BAC时,求∠BAD的度数.
(2)若AC⊥DE时,AC与DE交于点F,求旋转角的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
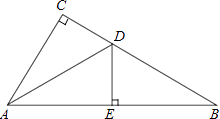
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,反比例函数y=
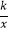 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点. 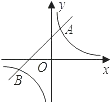
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了配合“八荣八耻”宣传教育,针对闯红灯的现象时有发生的实际情况,八年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早.中.晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志. 数据汇总如下:
部分时段车流量情况调查表
时间
负责组别
车流总量
每分钟车流量
早晨上学6:30~7:00
①②
2747
92
中午放学11:20~11:50
③④
1449
48
下午放学5:00~5:30
⑤⑥
3669
122
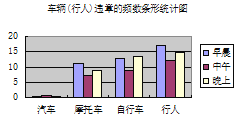
回答下列问题:
(1)请你写出2条交通法规.
(2)早晨.中午.晚上三个时段每分钟车流量的极差是多少,这三个时段的车流总量的中位数是多少.
(3)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因.
(4)通过分析写一条合理化建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①在△ABC中,点D是BC边上的一点,将△ABD沿AD折叠,得到△AED,AE与BC交于点F.已知∠B=50°,∠BAD=15°,求∠AFC的度数.
(2)如图②,将△ABC纸片沿DE折叠,使点A落在四边形BCED的内部点A′的位置,∠1、∠2与∠A之间存在一定的数量关系,请判断它们之间的关系,并说明理由.
(3)如图③,将△ABC纸片沿DE折叠,使点A落在四边形BCED的外部点A′的位置,此时∠1、∠2与∠A之间也存在一定的数量关系,请直接写出它们之间的关系,无需说明理由.

相关试题

