【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

参考答案:
【答案】(1)13;(2)△ABC的形状为直角三角形.
【解析】(1)用长方形的面积减去三个小三角形的面积即可求出△ABC的面积.
(2)根据勾股定理求得△ABC各边的长,再利用勾股定理的逆定理进行判定,从而不难得到其形状.
解:(1)△ABC 的面积=4 ×8-1 ×8 ÷2-2 ×3 ÷2-6 ×4 ÷2=13
故△ABC 的面积为13;
(2)∵正方形小方格边长为1
∴AC=![]() ,
, ![]() ,
, ![]()
∵在△ABC 中,AB2+BC2=13+52=65 ,AC2=65,
∴AB2+BC2=AC2,
∴网格中的△ABC是直角三角形.
“点睛”考查了三角形的面积,勾股定理和勾股定理的逆定理,解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则
 =__________,
=__________, =_________________ .
=_________________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家去体育场锻炼,同时,妈妈从体育场以50米/分的速度回家,小明到体育场后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图像.
(注:小明和妈妈始终在同一条笔直的公路上行走,图像上A、C、D三点在一条直线上)
(1)求线段BC的函数表达式;
(2)求点D坐标;
(3)当 x的值为 时,小明与妈妈相距1 500米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为________cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,∠BAD和∠DCB的平分线AE、CF分别交BC、AD于点E、F,点M、N分别为AE、CF的中点,连接FM、EN.试判断FM和EN的数量关系和位置关系,并加以证明.
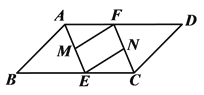
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示, AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.

-
科目: 来源: 题型:
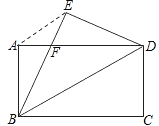
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
求证:(1)BF=DF;
(2)AE∥BD;
(3)若AB=6,AD=8,求BF的长.
相关试题

