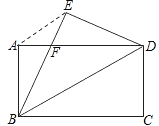
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
求证:(1)BF=DF;
(2)AE∥BD;
(3)若AB=6,AD=8,求BF的长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)BF的长为 ![]() .
.
【解析】试题分析:(1)由矩形的性质和折叠的性质可得到∠ADB=∠EBD,从而得BF=DF;
(2)根据矩形的性质和三角形内角可得∠AEB=∠FBD,再根据平行线的判定即可得;
(3)在Rt△ABF中 ,设BF=FD=![]() ,则AF
,则AF ![]() ,利用勾股定理即可得.
,利用勾股定理即可得.
试题解析:(1)在矩形ABCD中,AD∥BC,AD=BC,∴ ∠DBC=∠ADB,
∵ ∠DBC=∠EBD ,∴ ∠ADB=∠EBD,∴ BF=FD;
(2)∵ AD=BC=BE ,BF=DF ,∴ AF=EF,∴ ∠AEB=∠EAF,
∵ ∠AFE=∠BFD ,∠FBD=∠FDB,∴ ∠AEB=∠EBD, ∴ AE∥BD;
(3)在Rt△ABF中 ,设BF=FD=![]() ,则AF
,则AF ![]() ,则
,则
![]() ,解得:
,解得: ![]() , ∴ BF的长为
, ∴ BF的长为 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,∠BAD和∠DCB的平分线AE、CF分别交BC、AD于点E、F,点M、N分别为AE、CF的中点,连接FM、EN.试判断FM和EN的数量关系和位置关系,并加以证明.
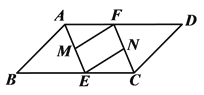
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示, AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个平面直角坐标系中第三象限内点的坐标:( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求梯形ABCE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】光年是一种长度单位,它表示光在一年中所通过的距离,已知光每秒的速度为3×105千米,一年以3×107秒计算,一光年约为( )
A.3×1012千米
B.9×1015千米
C.9×1035千米
D.9×1012千米
相关试题

