【题目】一艘轮船以每小时20千米的速度从甲港驶往160千米远的乙港,2小时后,一艘快艇以每小时40千米的速度也从甲港驶往乙港.分别列出轮船和快艇行驶的路程y(千米)与时间x(小时)的函数关系式,在下图中的直角坐标系中画出函数图象,观察图象回答下列问题:
(1)何时轮船行驶在快艇的前面?
(2)何时快艇行驶在轮船的前面?
(3)哪一艘船先驶过60千米?哪一艘船先驶过100千米?

参考答案:
【答案】(1)x<4小时时(2)4小时后(3)轮船先驶过60千米,快艇先驶过100千米.
【解析】试题分析:运用待定系数法分别求函数关系式;解方程组求交点坐标,结合图象回答(1)、(2)两个问题;(3)直接观察图象即可回答即可.
解:设快艇的函数关系式为y1=kx+b.
∵图象过(2,0)、(6,160),
∴![]() ,
,
解得![]() .
.
∴y1=40x-80.
同理可求轮船的函数关系式为y2=20x.
当y1=y2时,40x-80=20x,解得 x=4.
即x=4时,快艇追上轮船.
观察图象可知:
(1)轮船行使4小时之前,轮船行驶在快艇的前面;
(2)轮船行使4小时之后,快艇行驶在轮船的前面;
(3)轮船先驶过60千米,快艇先驶过100千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4>=5,<-1.5>=-1.
解决下列问题:
(1)[-4.5]=___,<3.5>=___;
(2)若[x]=2,则x的取值范围是___;若<y>=-1,则y的取值范围是___.
(3)已知x,y满足方程组
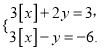 求x,y的取值范围.
求x,y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知△ABC中,∠C=90°,∠A=30°,AC=
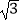 .动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .
.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 . 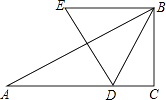
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.(1)在上述三个论断中,以其中两个论断作为条件,另外一个论断作结论,写出一个正确的命题,并加以证明。
命题:如果____________________那么____________________
证明:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( )

A. 5 B. 6 C. 7 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】有以下四个命题:
①反比例函数y=
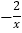 ,当x>0时,y随x的增大而增大;
,当x>0时,y随x的增大而增大;②抛物线y=x2﹣2x+2与两坐标轴无交点;
③平分弦的直径垂直于弦,且平分弦所对的弧;
④有一个角相等的两个等腰三角形相似.
其中正确命题的个数为( )
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 并将它的解集在数轴上表示出来.
并将它的解集在数轴上表示出来.
相关试题

