【题目】用配方法解方程.
(1) 3x2-4x-2=0; (2)x2-4![]() x+6=0.
x+6=0.
参考答案:
【答案】(1)原方程的解为x1=![]() , x2=
, x2=![]() ;(2)x=3
;(2)x=3![]() 或x=
或x=![]() .
.
【解析】
(1)方程移项,配方后,开方即可求出解.
(2)方程移项,配方后,开方即可求出解.
(1)将常数项移到方程右边 3x2-4x=2
将二次项系数化为1:x2-![]() x=
x=![]()
方程两边都加上一次项系数一半的平方:x2-![]() x+(
x+(![]() )2=
)2=![]() +(
+(![]() )2
)2
配方:(x-![]() )2=
)2=![]()
直接开平方得:x-![]() =
=![]()
∴x=![]()
∴原方程的解为x1=![]() , x2=
, x2=![]() ;
;
(2)将常数项移到方程右边x2-4![]() x=-6.
x=-6.
两边都加“一次项系数一半的平方”![]() =(2
=(2![]() )2,得
)2,得
x2-4![]() x+(2
x+(2![]() )2=-6+(2
)2=-6+(2![]() )2.
)2.
(x-2![]() )2=2,
)2=2,
用直接开平方法,得
x-2![]() =±
=±![]() ,
,
∴ x=3![]() 或x=
或x=![]() .
.
-
科目: 来源: 题型:
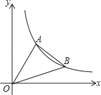
查看答案和解析>>【题目】如图,直线y=
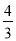 x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=
x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=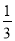 .
.(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)求S△OAB.
-
科目: 来源: 题型:
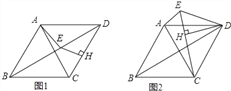
查看答案和解析>>【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是 ;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.

(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1)的值与字母x所取的值无关,代数式
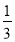 a2﹣2b2﹣(
a2﹣2b2﹣(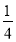 a3﹣3b2)=_____
a3﹣3b2)=_____ -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售甲、乙两种商品,现有如下信息:
请结合以上信息,解答下列问题:
(1)求甲、乙两种商品的进货单价;
(2)已知甲、乙两种商品的零售单价分别为2元、3元,该商店平均每天卖出甲商品500件和乙商品1300件,经市场调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商店决定把甲种商品的零售单价下降m(m>0)元,在不考虑其他因素的条件下,求当m为何值时,商店每天销售甲、乙两种商品获取的总利润为1800元(注:单件利润=零售单价﹣进货单价)

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一个内角为90°,且对角线相等的四边形称为“不完全矩形”.
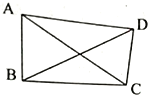
(1)①如图1,在不完全矩形
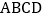 中,
中,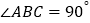 ,若
,若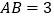 ,
,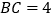 ,则
,则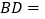 ____;
____;
②如图2,在平面直角坐标系中,
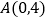 ,
,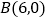 ,若整点
,若整点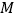 使得四边形
使得四边形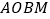 是不完全矩形,则点
是不完全矩形,则点 的坐标是_____;(整点指横坐标、纵坐标都为整数的点)
的坐标是_____;(整点指横坐标、纵坐标都为整数的点)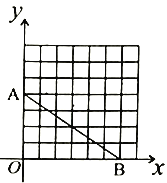
(2)如图3,在正方形
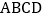 中,点
中,点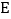 ,
,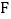 分别是
分别是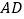 ,
,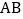 上的点,且
上的点,且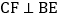 ,求证:四边形
,求证:四边形 是不完全矩形.
是不完全矩形.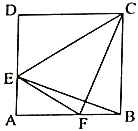
相关试题

