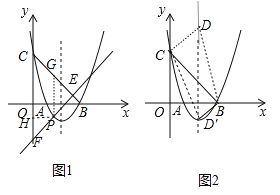
【题目】如图,抛物线![]() 与x轴交于A,B两点,B点坐标为(3,0).与y轴交于点C(0,3).
与x轴交于A,B两点,B点坐标为(3,0).与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值;
(3)点D为抛物线对称轴上一点.
①当△BCD是以BC为直角边的直角三角形时,求点D的坐标;
②若△BCD是锐角三角形,求点D的纵坐标的取值范围.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①D点坐标为(2,5)或(2,﹣1);②点D的纵坐标的取值范围为
;(3)①D点坐标为(2,5)或(2,﹣1);②点D的纵坐标的取值范围为![]() <y<5或﹣1<y<
<y<5或﹣1<y<![]() .
.
【解析】试题分析:(1)利用待定系数法求抛物线的解析式;
(2)易得BC的解析式为y=﹣x+3,先证明△ECF为等腰直角三角形,作PH⊥y轴于H,PG∥y轴交BC于G,如图1,则△EPG为等腰直角三角形,PE=![]() PG,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),接着利用t表示PF、PE,所以PE+EF=2PE+PF=
PG,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),接着利用t表示PF、PE,所以PE+EF=2PE+PF= ![]() ,然后利用二次函数的性质解决问题;
,然后利用二次函数的性质解决问题;
(3)①如图2,抛物线的对称轴为直线x=2,设D(2,y),利用两点间的距离公式得到BC2=18,DC2=4+(y﹣3)2,BD2=1+y2,讨论:当△BCD是以BC为直角边,BD为斜边的直角三角形时,18+4+(y﹣3)2=1+y2;当△BCD是以BC为直角边,CD为斜边的直角三角形时,4+(y﹣3)2=1+y2+18,分别解方程求出t即可得到对应的D点坐标;
②由于△BCD是以BC为斜边的直角三角形有4+(y﹣3)2+1+y2=18,解出y的值,得到此时D点的坐标,然后结合图形可确定△BCD是锐角三角形时点D的纵坐标的取值范围.
试题解析:解:(1)把B(3,0),C(0,3)代入![]() 得:
得: ![]() ,解得:
,解得: ![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ;
;
(2)易得BC的解析式为y=﹣x+3,∵直线y=x﹣m与直线y=x平行,∴直线y=﹣x+3与直线y=x﹣m垂直,∴∠CEF=90°,∴△ECF为等腰直角三角形,作PH⊥y轴于H,PG∥y轴交BC于G,如图1,△EPG为等腰直角三角形,PE=![]() PG,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),∴PF=
PG,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),∴PF=![]() PH=
PH=![]() t,PG=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,∴PE=
t,PG=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,∴PE=![]() PG=
PG= ![]() ,∴PE+EF=PE+PE+PF=2PE+PF=
,∴PE+EF=PE+PE+PF=2PE+PF= ![]() =
= ![]() =
=![]() ,当t=2时,PE+EF的最大值为
,当t=2时,PE+EF的最大值为![]() ;
;
(3)①如图2,抛物线的对称轴为直线x=![]() =2,设D(2,y),则BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,当△BCD是以BC为直角边,BD为斜边的直角三角形时,BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,解得y=5,此时D点坐标为(2,5);
=2,设D(2,y),则BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,当△BCD是以BC为直角边,BD为斜边的直角三角形时,BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,解得y=5,此时D点坐标为(2,5);
当△BCD是以BC为直角边,CD为斜边的直角三角形时,BC2+DB2=DC2,即4+(y﹣3)2=1+y2+18,解得y=﹣1,此时D点坐标为(2,﹣1);
综上所述:D点坐标为(2,5)或(2,﹣1).
②当△BCD是以BC为斜边的直角三角形时,DC2+DB2=BC2,即4+(y﹣3)2+1+y2=18,解得y1=![]() ,y2=
,y2=![]() ,此时D点坐标为(2,
,此时D点坐标为(2, ![]() )或(2,
)或(2, ![]() ),所以△BCD是锐角三角形,点D的纵坐标的取值范围为
),所以△BCD是锐角三角形,点D的纵坐标的取值范围为![]() <y<5或﹣1<y<
<y<5或﹣1<y<![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式x﹣2y的值是5,则代数式﹣3x+6y+1的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,
 ,
, 
(1)用尺规作图作AB边上中垂线DE,交AC于点D,交AB于点E。(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,CE,BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3……
第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为En.

(1)如图①,求证:∠E=∠B+∠C;
(2)如图②,求证:∠E1=
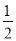 ∠E;
∠E;(3)猜想:若∠En=b°,求∠BEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,,直线MN分别与x轴、y轴交于点M(6,0),N(0,
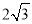 ),等边△ABC的顶点B与原点O重合,BC边落在x轴正半轴上,点A恰好落在线段MN上,将等边△ABC从图l的位置沿x轴正方向以每秒l个单位长度的速度平移,边AB,AC分别与线段MN交于点E,F(如图2所示),设△ABC平移的时间为t(s).
),等边△ABC的顶点B与原点O重合,BC边落在x轴正半轴上,点A恰好落在线段MN上,将等边△ABC从图l的位置沿x轴正方向以每秒l个单位长度的速度平移,边AB,AC分别与线段MN交于点E,F(如图2所示),设△ABC平移的时间为t(s).(1)等边△ABC的边长为_______;
(2)在运动过程中,当t=_______时,MN垂直平分AB;
(3)若在△ABC开始平移的同时.点P从△ABC的顶点B出发.以每秒2个单位长度的速度沿折线BA—AC运动.当点P运动到C时即停止运动.△ABC也随之停止平移.
①当点P在线段BA上运动时,若△PEF与△MNO相似.求t的值;
②当点P在线段AC上运动时,设
 ,求S与t的函数关系式,并求出S的最大值及此时点P的坐标.
,求S与t的函数关系式,并求出S的最大值及此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:(5a2+2a﹣1)﹣4(3﹣8a+2a2),其中a=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
①∠BOE=70°; ②OF平分∠BOD;③∠POE=∠BOF; ④∠POB=2∠DOF.
其中正确的结论有_______________(填结论前面的序号)

相关试题

