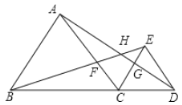
【题目】如图所示,是某城市街道示意图,已知![]() 与
与![]() 均是等边三角形(即三条边都相等,三个角都相等的三角形),点
均是等边三角形(即三条边都相等,三个角都相等的三角形),点![]() 为公交车停靠站,且点
为公交车停靠站,且点![]() 在同一条直线上.
在同一条直线上.
(1)图中![]() 与
与![]() 全等吗?请说明理由;
全等吗?请说明理由;
(2)连接![]() ,写出
,写出![]() 与
与![]() 的大小关系;
的大小关系;
(3)公交车甲从![]() 出发,按照
出发,按照![]() 的顺序到达
的顺序到达![]() 站;公交车乙从
站;公交车乙从![]() 出发,按照
出发,按照![]() 的顺序到达
的顺序到达![]() 站.若甲,乙两车分别从
站.若甲,乙两车分别从![]() 两站同时出发,在各站停靠的时间相同,两车的平均速度也相同,则哪一辆公交车先到达指定站?为什么?
两站同时出发,在各站停靠的时间相同,两车的平均速度也相同,则哪一辆公交车先到达指定站?为什么?
参考答案:
【答案】(1)![]() ,见解析;(2)
,见解析;(2)![]() ;(3)两公交车同时到达指定站,见解析
;(3)两公交车同时到达指定站,见解析
【解析】
(1)根据SAS判定![]() ;
;
(2)先证明![]() 即可判定
即可判定![]() 与
与![]() 的大小关系;
的大小关系;
(3)利用等边三角形的性质及全等三角形的对应边相等,从而推出两车同时到达.
解:(1)![]() ,
,
理由如下:
因为![]() 与
与![]() 均是等边三角形,
均是等边三角形,
所以![]() ,
,![]() ,
,![]() .
.
所以![]() ,即
,即![]() .
.
在![]() 和
和![]() 中,因为
中,因为![]() ,
,![]() ,
,![]() .
.
所以![]() .
.
(2)如图,连接![]()
由(1) ![]()
∴![]()
∵![]()
![]()
∵![]()
∴![]()
∴![]()
∴![]()
(3)公交车甲行驶路程为:![]() .
.
公交车乙行驶路程为:![]() .
.
由(1)知![]() ,
,![]() ,
,
所以![]() ,(全等三角形的对应边相等).
,(全等三角形的对应边相等).
所以两车行驶的路程相等.
因为甲,乙两车分别从![]() 两站同时出发,行驶的路程相等,在各站停靠的时间相同,两车的平均速度也相同,所以两公交车同时到达指定站.
两站同时出发,行驶的路程相等,在各站停靠的时间相同,两车的平均速度也相同,所以两公交车同时到达指定站.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量y(万件)与月份x(月)的关系为:
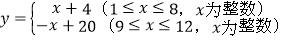 ,每件产品的利润z(元)与月份x(月)的关系如下表:
,每件产品的利润z(元)与月份x(月)的关系如下表:x
1
2
3
4
5
6
7
8
9
10
11
12
z
19
18
17
16
15
14
13
12
11
10
10
10
(1)请你根据表格求出每件产品利润z(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:如果两个一次函数的一次项系数和常数项互换,即y=kx+b和y=bx+k(其中|k|≠|b|),称这样的两个一次函数为互助一次函数,例如
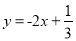 和
和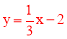 就是互助一次函数.根据规定解答下列问题:
就是互助一次函数.根据规定解答下列问题:(1)填空:一次函数
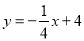 与它的互助一次函数的交点坐标为______
与它的互助一次函数的交点坐标为______(2)若两个一次函数y=(k-b)x – k - 2b与
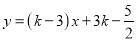 是互助一次函数,求两函数图象与y轴围成的三角形的面积.
是互助一次函数,求两函数图象与y轴围成的三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】将长为
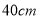 ,宽为
,宽为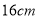 的长方形白纸,按图示方法粘合起来,粘合部分宽为
的长方形白纸,按图示方法粘合起来,粘合部分宽为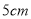 .
.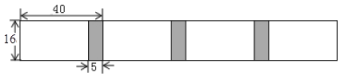
(1)根据图示,将下表补充完整;
白纸张数
1
2
3
4
5
…
纸条长度/
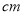
40
110
145
…
(2)设
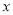 张白纸粘合后的总长度为
张白纸粘合后的总长度为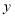 ,求
,求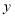 与
与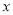 之间的关系式;
之间的关系式;(3)将若干张白纸按上述方式粘合起来,你认为总长度可能为
 吗?为什么?
吗?为什么? -
科目: 来源: 题型:
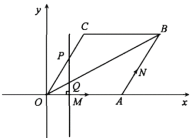
查看答案和解析>>【题目】如图,在直角坐标系XOY中,菱形OABC的边OA在x轴正半轴上,点B,C在第一象限,∠C=120°,边长OA=8,点M从原点O出发沿x轴正半轴以每秒1个单位长的速度作匀速运动,点N从A出发沿边AB—BC—CO以每秒2个单位长的速度作匀速运动.过点M作直线MP垂直于x轴并交折线OCB于P,交对角线OB于Q,点M和点N同时出发,分别沿各自路线运动,点N运动到原点O时,M和N两点同时停止运动.
(1)当t=2时,求线段PQ的长;
(2)求t为何值时,点P与N重合;
(3)设△APN的面积为S,求S与t的函数关系式及t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:
(1)作线段AB,分别以A,B为圆心,以AB长为半径作弧,两弧的交点为C;
(2)以C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
(3)连接BD,BC.
下列说法不正确的是( )

A. ∠CBD=30° B. S△BDC=
 AB2
AB2C. 点C是△ABD的外心 D. sin2A+cos2D=l
-
科目: 来源: 题型:
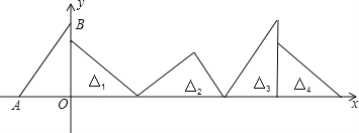
查看答案和解析>>【题目】 如图,在直角坐标系中,已知点A(-3,0),B(0,4),AB=5,对△OAB连续做旋转变换,依次得到△1,△2,△3,△4,…,则△2017的直角顶点的坐标为______.
相关试题

