【题目】在平面直角坐标系中,O是坐标原点,A(2,2),B(4,﹣3),P是x轴上的一点.
(1)若PA+PB的值最小,求P点的坐标;
(2)若∠APO=∠BPO.
①求此时P点的坐标;
②在y轴上是否存在点Q,使得△QAB的面积等于△PAB的面积,若存在,求出Q点坐标;若不存在,说明理由.
参考答案:
【答案】(1)P点坐标为(![]() ,0);(2)①点P坐标为(﹣2,0);②y轴上存在点Q使得△QAB的面积等于△PAB的面积,Q的坐标为(0,﹣5)或(0,19).
,0);(2)①点P坐标为(﹣2,0);②y轴上存在点Q使得△QAB的面积等于△PAB的面积,Q的坐标为(0,﹣5)或(0,19).
【解析】
(1)根据题意画坐标系描点,根据两点之间线段最短,求直线AB解析式,与x轴交点即为所求点P.
(2)①作点A关于x轴的对称点A',根据轴对称性质有∠APO=∠A'PO,所以此时P、A'、B在同一直线上.求直线A'B解析式,与x轴交点即为所求点P.
②法一,根据坐标系里三角形面积等于水平长(右左两顶点的横坐标差)与铅垂高(上下两顶点的纵坐标差)乘积的一半,求得△PAB的面积为12,进而求得△QAP的铅垂高等于6,再得出直线BQ上的点E坐标为(2,8)或(2,﹣4),求出直线BQ,即能求出点Q坐标.法二,根据△QAB与△PAB同以AB为底时,高应相等,所以点Q在平行于直线AB、且与直线AB距离等于P到直线AB距离的直线上.这样的直线有两条,一条即过点P且与AB平行的直线,另一条在AB上方,根据平移距离相等即可求出.所求直线与y轴交点即点Q.
(1)∵两点之间线段最短,∴当A、P、B在同一直线时,PA+PB=AB最短(如图1).
设直线AB的解析式为:y=kx+b.
∵A(2,2),B(4,﹣3),∴![]() ,解得:
,解得: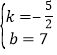 ,∴直线AB:y
,∴直线AB:y![]() x+7.
x+7.
当![]() x+7=0时,得:x
x+7=0时,得:x![]() ,∴P点坐标为(
,∴P点坐标为(![]() ,0).
,0).
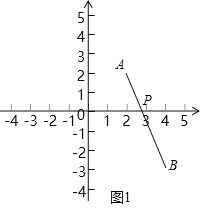
(2)①作点A(2,2)关于x轴的对称点A'(2,﹣2).
根据轴对称性质有∠APO=∠A'PO.
∵∠APO=∠BPO,∴∠A'PO=∠BPO,∴P、A'、B在同一直线上(如图2).
设直线A'B的解析式为:y=k'x+b'.
![]() ,解得:
,解得: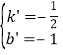 ,∴直线A'B:y
,∴直线A'B:y![]() x﹣1.
x﹣1.
当![]() x﹣1=0时,得:x=﹣2,∴点P坐标为(﹣2,0).
x﹣1=0时,得:x=﹣2,∴点P坐标为(﹣2,0).
②存在满足条件的点Q.
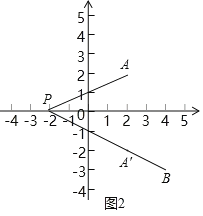
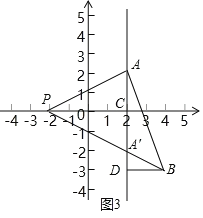
法一:设直线AA'交x轴于点C,过B作BD⊥直线AA'于点D(如图3),∴PC=4,BD=2,∴S△PAB=S△PAA'+S△BAA'![]() .
.
设BQ与直线AA'(即直线x=2)的交点为E(如图4).
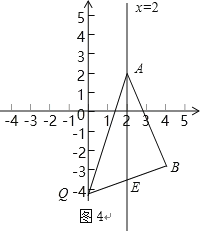
∵S△QAB=S△PAB,则S△QAB![]() 2AE=12,∴AE=6,∴E的坐标为(2,8)或(2,﹣4).
2AE=12,∴AE=6,∴E的坐标为(2,8)或(2,﹣4).
设直线BQ解析式为:y=ax+q.则:
![]() 或
或![]()
解得: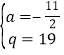 或
或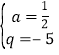 ,∴直线BQ:y
,∴直线BQ:y![]() 或y
或y![]() ,∴Q点坐标为(0,19)或(0,﹣5).
,∴Q点坐标为(0,19)或(0,﹣5).
法二:∵S△QAB=S△PAB,∴△QAB与△PAB以AB为底时,高相等,即点Q到直线AB的距离=点P到直线AB的距离.
i)若点Q在直线AB下方,则PQ∥AB.
设直线PQ:y![]() x+c,把点P(﹣2,0)代入,解得:c=﹣5,y
x+c,把点P(﹣2,0)代入,解得:c=﹣5,y![]() x﹣5,即Q(0,﹣5);
x﹣5,即Q(0,﹣5);
ii)若点Q在直线AB上方.
∵直线y![]() x﹣5向上平移12个单位得直线AB:y
x﹣5向上平移12个单位得直线AB:y![]() x+7,∴把直线AB:y
x+7,∴把直线AB:y![]() x+7再向上平移12个单位得直线AB:y
x+7再向上平移12个单位得直线AB:y![]() x+19,∴Q(0,19).
x+19,∴Q(0,19).
综上所述:y轴上存在点Q使得△QAB的面积等于△PAB的面积,Q的坐标为(0,﹣5)或(0,19).
-
科目: 来源: 题型:
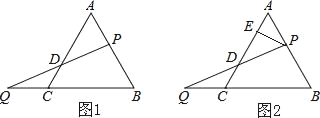
查看答案和解析>>【题目】P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D.
(1)证明:PD=DQ.
(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄
清理养鱼网箱人数/人
清理捕鱼网箱人数/人
总支出/元
A
15
9
57000
B
10
16
68000
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 , ∠AFB=∠ .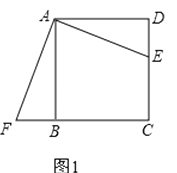
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ.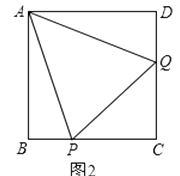
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.
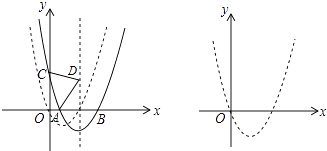
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△ PAC为等边三角形,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD沿直线AC对折后重合,如果AC,BD交于O,AB∥CD,则结论①AB=CD,②AD∥BC,③AC⊥BD,④AO=CO,⑤AB⊥BC,其中正确的结论是___(填序号).
相关试题

