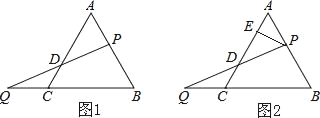
【题目】P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D.
(1)证明:PD=DQ.
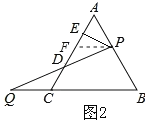
(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.
参考答案:
【答案】(1)证明见解析;(2)DE=3.
【解析】
(1)过点P作PF∥BC交AC于点F;证出△APF也是等边三角形,得出AP=PF=AF=CQ,由AAS证明△PDF≌△QDC,得出对应边相等即可;
(2)过P作PF∥BC交AC于F.同(1)由AAS证明△PFD≌△QCD,得出对应边相等FD=CD,证出AE+CD=DE![]() AC,即可得出结果.
AC,即可得出结果.
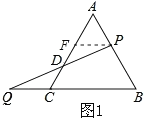
(1)如图1所示,点P作PF∥BC交AC于点F.
∵△ABC是等边三角形,∴△APF也是等边三角形,AP=PF=AF=CQ.
∵PF∥BC,∴∠PFD=∠DCQ.
在△PDF和△QDC中,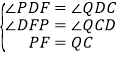 ,∴△PDF≌△QDC(AAS),∴PD=DQ;
,∴△PDF≌△QDC(AAS),∴PD=DQ;
(2)如图2所示,过P作PF∥BC交AC于F.
∵PF∥BC,△ABC是等边三角形,∴∠PFD=∠QCD,△APF是等边三角形,∴AP=PF=AF.
∵PE⊥AC,∴AE=EF.
∵AP=PF,AP=CQ,∴PF=CQ.
在△PFD和△QCD中,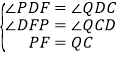 ,∴△PFD≌△QCD(AAS),∴FD=CD.
,∴△PFD≌△QCD(AAS),∴FD=CD.
∵AE=EF,∴EF+FD=AE+CD,∴AE+CD=DE![]() AC.
AC.
∵AC=6,∴DE=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.
(1)求出y与x的函数关系式
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?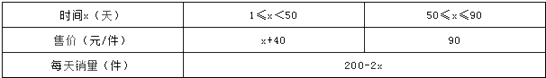 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D在AB上,点E在BC上,BD=BE.
(1)请你再添加一个条件,使得△BEA≌△BDC,并给出证明.你添加的条件是 .
(2)根据你添加的条件,再写出图中的一对全等三角形 .(只要求写出一对全等三角形,不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄
清理养鱼网箱人数/人
清理捕鱼网箱人数/人
总支出/元
A
15
9
57000
B
10
16
68000
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O是坐标原点,A(2,2),B(4,﹣3),P是x轴上的一点.
(1)若PA+PB的值最小,求P点的坐标;
(2)若∠APO=∠BPO.
①求此时P点的坐标;
②在y轴上是否存在点Q,使得△QAB的面积等于△PAB的面积,若存在,求出Q点坐标;若不存在,说明理由.
相关试题

