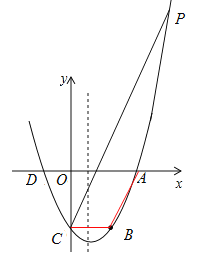
【题目】如图,已知抛物线y=![]() x2-
x2-![]() x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.

(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)A点坐标为(4,0),D点坐标为(-2,0),C点坐标为(0,-3);
(2)M点坐标为(2,-3)或(1+![]() ,3)或(1-
,3)或(1-![]() ,3);
,3);
(3)在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(-2,0)或(6,6).
【解析】试题分析:(1)在![]() 中令
中令![]() ,解得
,解得![]() ,
,
∴A(4,0) 、D(-2,0).
在![]() 中令
中令![]() ,得
,得![]() ,∴C(0,-3).
,∴C(0,-3).
(2)连接AC,根据轴对称的性质,AC与抛物线的对称轴交点M即为所求,从而应用待定系数法求出AC的解析式,再求出抛物线的对称轴,即可求得点M的坐标.
(3)分BC为梯形的底边和BC为梯形的腰两种情况讨论即可.
试题解析:(1)A(4,0) 、D(-2,0)、C(0,-3)
(2)如图,连接AC,则AC与抛物线的对称轴交点M即为所求.
设直线AC的解析式为![]() ,则
,则![]() ,解得
,解得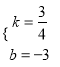 .
.
∴直线AC的解析式为![]() .
.
∵![]() 的对称轴是直线
的对称轴是直线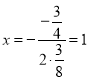 ,
,
把x=1代入![]() 得
得![]()
`∴M(1, ![]() ).
).
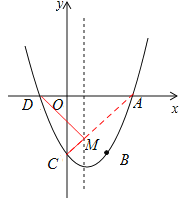
(3)存在,分两种情况:
①如图,当BC为梯形的底边时,点P与D重合时,四边形ADCB是梯形,此时点P为(-2,0).
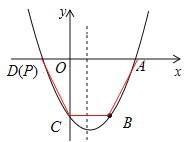
②如图,当BC为梯形的腰时,过点C作CP//AB,与抛物线交于点P,
∵点C,B关于抛物线对称,∴B(2,-3)
设直线AB的解析式为![]() ,则
,则![]() ,解得
,解得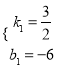 .
.
∴直线AB的解析式为![]() .
.
∵CP//AB,∴可设直线CP的解析式为![]() .
.
∵点C在直线CP上,∴![]() .
.
∴直线CP的解析式为![]() .
.
联立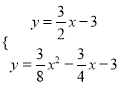 ,解得
,解得![]() ,
, ![]()
∴P(6,6).
综上所述,在抛物线上存在点P,使得以A、B、C、P四点为顶点的四边形为梯形,点P的坐标为(-2,0)或(6,6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.

利用数形结合思想回答下列问题:
①数轴上表示1和3两点之间的距离是
②数轴上表示x和-1的两点之间的距离表示为
③若x表示一个有理数,且-4<x<2,则|x-2|+|x+4|=
④若x表示一个有理数,且|x-2|+|x+4|=8,则有理数x的值是
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(+17)+(-12);
(2)10+(―
 )―6―(―0.25);
)―6―(―0.25);(3)(
 )×48 ;
)×48 ;(4)|-5-4|-5×(-2)2-1÷(-
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.

(1)写出商场销售这种工具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
-
科目: 来源: 题型:
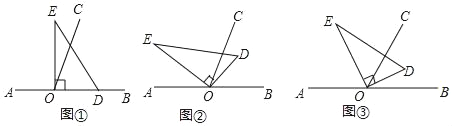
查看答案和解析>>【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 、
、 、
、 是数轴上三点,点
是数轴上三点,点 表示的数为3,
表示的数为3, ,
, 。
。
(1)数轴上点
 表示的数为,点
表示的数为,点 表示的数为。
表示的数为。(2)动点
 、
、 分别从
分别从 、
、 同时出发,点
同时出发,点 以每秒2个单位长度的速度沿数轴向右匀速运动,点
以每秒2个单位长度的速度沿数轴向右匀速运动,点 以每秒1个单位长度的速度沿数轴向左匀速运动,
以每秒1个单位长度的速度沿数轴向左匀速运动, 为
为 的中点,点
的中点,点 在线段
在线段 上,且
上,且 ,设运动时间为
,设运动时间为 (
( )秒。
)秒。 ①求数轴上
 、
、 表示的数(用含
表示的数(用含 的式子表示);
的式子表示); ②
 为何值时,原点
为何值时,原点 恰好是线段
恰好是线段 的中点;
的中点;
相关试题

