【题目】如图,已知![]() 、
、![]() 、
、![]() 是数轴上三点,点
是数轴上三点,点![]() 表示的数为3,
表示的数为3,![]() ,
,![]() 。
。
![]()
(1)数轴上点![]() 表示的数为,点
表示的数为,点![]() 表示的数为。
表示的数为。
(2)动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,点
同时出发,点![]() 以每秒2个单位长度的速度沿数轴向右匀速运动,点
以每秒2个单位长度的速度沿数轴向右匀速运动,点![]() 以每秒1个单位长度的速度沿数轴向左匀速运动,
以每秒1个单位长度的速度沿数轴向左匀速运动,![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() ,设运动时间为
,设运动时间为![]() (
(![]() )秒。
)秒。
①求数轴上![]() 、
、![]() 表示的数(用含
表示的数(用含![]() 的式子表示);
的式子表示);
②![]() 为何值时,原点
为何值时,原点![]() 恰好是线段
恰好是线段![]() 的中点;
的中点;
参考答案:
【答案】(1)-5,1;(2)①M表示的数是-5+t;N表示的数是3-![]() t;②当t=2秒时,O为PQ的中点.
t;②当t=2秒时,O为PQ的中点.
【解析】
(1)根据点C所表示的数,以及BC、AB的长度,即可写出点A、B表示的数;
(2)①根据题意画出图形,表示出AP=6t,CQ=3t,再根据线段的中点定义可得AM=3t,根据线段之间的和差关系进而可得到点M表示的数;根据CN=![]() CQ可得CN=t,根据线段的和差关系可得到点N表示的数;
CQ可得CN=t,根据线段的和差关系可得到点N表示的数;
②此题有两种情况:当点P在点O的左侧,点Q在点O的右侧时;当P在点O的右侧,点Q在点O的左侧时,分别画出图形进行计算即可.
解:(1)∵C表示的数为3,BC=2,
∴OB=3-2=1,
∴B点表示1.
∵AB=6,
∴AO=6-1=5,
∴A点表示-5;
(2)①由题意得:AP=2t,CQ=t,如图1所示:
,
∴AM=![]() ,AM=t,
,AM=t,
∴在数轴上点M表示的数是-5+t,,
∵点N在CQ上,CN=![]() CQ,∴CN=
CQ,∴CN=![]() t,
t,
∴在数轴上点N表示的数是3-![]() t;
t;
②如图2所示:由题意得,AP=3t,CQ=t,分两种情况:
i)当点P在点O的左侧,点Q在点O的右侧时,OP=5-2t,OQ=3-t,
![]()
∵O为PQ的中点,
∴OP=OQ,
∴5-2t=3-t,
解得:t=2,当t=2秒时,O为PQ的中点;
ii)当P在点O的右侧,点Q在点O的左侧时,OP=2t-5,OQ=t-3,
![]()
∵O为PQ的中点,
∴OP=OQ,
∴2t-5=t-3,解得:t=2,此时0P=-1<0,线段不能为负,舍去,
综上所述:当t=2秒时,O为PQ的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2-
x2- x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
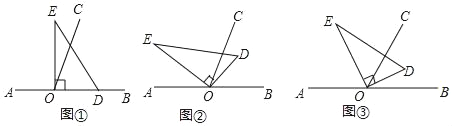
查看答案和解析>>【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
-
科目: 来源: 题型:
查看答案和解析>>【题目】温州市处于东南沿海,夏季经常遭受台风袭击.一次,温州气象局测得台风中心在温州市A的正西方向300千米的B处(如图),以每小时10
 千米的速度向东偏南30°的BC方向移动,并检测到台风中心在移动过程中,温州市A将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市A的时间会持续多长?( )
千米的速度向东偏南30°的BC方向移动,并检测到台风中心在移动过程中,温州市A将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市A的时间会持续多长?( )
A. 5 B. 6 C. 8 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从4月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表:
一户居民一个月用电量的范围
电费价格(单位:元/度)
不超过150度

超过150度的部分

今年5月份,该市居民甲用电100度,交电费60元;居民乙用电200度,交电费122.5元.
(1)上表中,
 ,
, ;
;(2)试行“阶梯电价”收费以后,该市一户居民今年8月份平均电价每度为0.63元,求该用户8月用电多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).

相关试题

