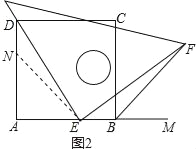
【题目】如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM的平分线BF相交于点F.

(1)如图1,当点E在AB边得中点位置时:
①通过测量DE、EF的长度,猜想DE与EF满足的数量关系是 .
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ,请证明你的猜想.
(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.
参考答案:
【答案】(1)①DE=EF;②NE=BF;理由见解析;(2)DE=EF,理由见解析.
【解析】试题分析:(1)根据正方形的性质及N,E分别为AD,AB的中点可得DN=EB,再根据角平分线的性质及AN=AE可得∠DNE=∠EBF=135°,从而可证得△DNE≌△EBF,继而证得结论;
(2)在DA边上截取DN=EB,连结NE,点N就使得NE=BF成立,由DN=EB可得AN=AE,根据角平分线的性质可得∠DNE=∠EBF=90°+45°=135°,通过证△DNE≌△EBF,从而得结论.
(1)①DE=EF;②NE=BF;理由如下:
∵四边形ABCD为正方形,∴AD=AB,∠DAB=∠ABC=90°,∵N,E分别为AD,AB中点,
∴AN=DN=![]() AD,AE=EB=
AD,AE=EB=![]() AB,∴DN=BE,AN=AE,∵∠DEF=90°,∴∠AED+∠FEB=90°,
AB,∴DN=BE,AN=AE,∵∠DEF=90°,∴∠AED+∠FEB=90°,
又∵∠ADE+∠AED=90°,∴∠FEB=∠ADE,又∵AN=AE,∴∠ANE=∠AEN,又∵∠A=90,∴∠ANE=45°,∴∠DNE=180°﹣∠ANE=135°,又∵∠CBM=90°,BF平分∠CBM,
∴∠CBF=45°,∠EBF=135°,在△DNE和△EBF中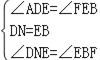 , ∴△DNE≌△EBF(ASA),∴DE=EF,NE=BF.
, ∴△DNE≌△EBF(ASA),∴DE=EF,NE=BF.
(2)DE=EF,理由如下:
在DA边上截取DN=EB,连接NE,∵四边形ABCD是正方形,DN=EB,∴AN=AE,∴△AEN为等腰直角三角形,∴∠ANE=45°,∴∠DNE=180°﹣45°=135°,∵BF平分∠CBM,AN=AE,∴∠EBF=90°+45°=135°,∴∠DNE=∠EBF, ∵∠NDE+∠DEA=90°,∠BEF+∠DEA=90°,∴∠NDE=∠BEF,在△DNE和△EBF中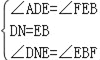 ,∴△DNE≌△EBF(ASA), ∴DE=EF.
,∴△DNE≌△EBF(ASA), ∴DE=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3a2=a5
B.a6÷a2=a3
C.(a3)2=a5
D.(3a)3=3a3 -
科目: 来源: 题型:
查看答案和解析>>【题目】平面内有三条直线,那么它们的交点个数有( )
A. 0个或1个B. 0个或2个C. 0个或1个或2个D. 0个或1个或2个或3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2x+3y=5xyB.(x+3)2=x2+9
C.(xy2)3=x3y6D.x10÷x5=x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣x2+3zx+xy)=﹣2x3+6x2z+2x2y.
-
科目: 来源: 题型:
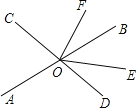
查看答案和解析>>【题目】直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,垂足为O.
(1)若∠EOF=54°,求∠AOC的度数;
(2)①在∠AOD的内部作射线OG⊥OE;
②试探索∠AOG与∠EOF之间有怎样的关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点).有下列结论:①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣
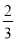 ;④
;④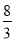 ≤n≤4.其中正确的是( )
≤n≤4.其中正确的是( )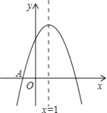
A. ①② B. ③④ C. ①③ D. ①③④
相关试题

