【题目】如图,在Rt△ABC中,∠C=90°,CA=12![]() cm,BC=12cm;动点P从点C开始沿CA以2
cm,BC=12cm;动点P从点C开始沿CA以2![]() cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.
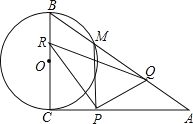
(1)∠CAB的度数是 ;
(2)以CB为直径的⊙O与AB交于点M,当t为何值时,PM与⊙O相切?
(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求S的最小值及相应的t值;
(4)是否存在△APQ为等腰三角形?若存在,求出相应的t值;若不存在请说明理由.
参考答案:
【答案】(1)30°;(2)t=3s时,PM与⊙O相切;(3)当t=3s时,![]() cm2;(4)当
cm2;(4)当![]() s时,△APQ是等腰三角形.
s时,△APQ是等腰三角形.
【解析】
试题分析:(1)根据题意和正切的定义以及特殊角的三角函数值解答即可;
(2)连接OP,OM,根据切线的性质得到∠PMO=90°,证明Rt△PMO≌Rt△PCO,△OBM是等边三角形,根据等边三角形的性质和正切的概念解答;
(3)过点Q作QE⊥AC于点E,根据余弦的概念用t表示出QE,根据三角形的面积公式和二次函数的性质解答;
(4)分PQ1=AQ1=4t、AP=AQ2=4t、PA=PQ3=4t三种情况,作出辅助线,根据等腰三角形的性质计算即可.
解:(1)∵∠C=90°,CA=12![]() cm,BC=12cm,
cm,BC=12cm,
∴tan∠CAB=![]() =
=![]() ,
,
∴∠CAB=30°,
故答案为:30°;
(2)如图1,连接OP,OM.
当PM与⊙O相切时,有∠PMO=∠PCO=90°,
∵MO=CO,PO=PO,
∴Rt△PMO≌Rt△PCO,
∴∠MOP=∠COP;
由(1)知∠OBA=60°,
∵OM=OB,
∴△OBM是等边三角形,
∴∠BOM=60°,
∴∠MOP=∠COP=60°,
∴CP=COtan∠COP=6tan60°=![]() ,
,
又∵![]()
∴![]() t=
t=![]()
∴t=3,
即:t=3s时,PM与⊙O相切;
(3)如图2,过点Q作QE⊥AC于点E,
∵∠BAC=30°,AQ=4t,
∴![]() AE=AQcos∠BAC=4tcos30°=
AE=AQcos∠BAC=4tcos30°=![]() ,
,
∴![]()
![]()
![]() =
=![]()
![]() =
=![]() ;
;
∴S△PQR=S△ACB﹣S△AQP﹣S△QBR﹣S△PCR
=![]()
=![]()
=![]() (0<t<6),
(0<t<6),
∴当t=3s时,![]() cm2;
cm2;
(4)存在.如图3,分三种情况:
①PQ1=AQ1=4t时,过点Q1作Q1D⊥AC于点D,
则![]()
![]() ,
,
∴![]() ,
,
∴t=2;
②当AP=AQ2=4t时,
∵![]() ,
,
∴![]()
![]() =
=![]() ,
,
③当PA=PQ3=4t时,
过点P作PH⊥AB于点H,
AH=PAcos30°=![]() =18﹣3tAQ3=2AH=36﹣6t,
=18﹣3tAQ3=2AH=36﹣6t,
∴36﹣6t=4t,
∴t=3.6,
综上所述,当![]() s时,△APQ是等腰三角形.
s时,△APQ是等腰三角形.



-
科目: 来源: 题型:
查看答案和解析>>【题目】几何知识可以解决生活中许多距离最短的问题.让我们从书本一道习题入手进行知识探索.
【回忆】
如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并说明理由.

【探索】
(1)如图,A、B两个村庄在一条笔直的马路的两端,村庄 C在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置,并说明理由.

(2)如图,A、B、C、D四个村庄,现建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O的位置,并说明理由.
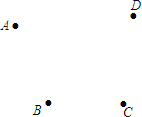
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣3x+k与x轴交于A、B两点,与y轴交于点C(0,﹣4).

(1)k= ;
(2)点A的坐标为 ,B的坐标为 ;
(3)设抛物线y=x2﹣3x+k的顶点为M,求四边形ABMC的面积.
-
科目: 来源: 题型:
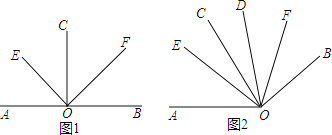
查看答案和解析>>【题目】(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= .(用含α与β的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOC=∠BOD=α(0°<α<180°)
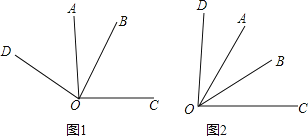
(1)如图1,若α=90°
①写出图中一组相等的角(除直角外) ,理由是
②试猜想∠COD和∠AOB在数量上是相等、互余、还是互补的关系,并说明理由;
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是 ;当α= °,∠COD和∠AOB互余.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b互为相反数,c、d互为倒数,m是绝对值等于3的负数,则m2+(cd+a+b)×m+(cd)2009的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
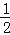 x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣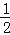 x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).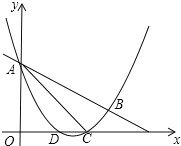
(Ⅰ)求抛物线的解析式和tan∠BAC的值;
(Ⅱ)在(Ⅰ)条件下,P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
相关试题

