【题目】几何知识可以解决生活中许多距离最短的问题.让我们从书本一道习题入手进行知识探索.
【回忆】
如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并说明理由.

【探索】
(1)如图,A、B两个村庄在一条笔直的马路的两端,村庄 C在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置,并说明理由.

(2)如图,A、B、C、D四个村庄,现建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O的位置,并说明理由.
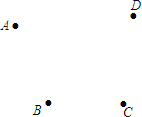
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
试题分析:【回忆】根据两点之间线段最短即可确定;
【探索】(1)根据垂线段最短即可解答;
(2)根据两点之间线段最短即可解答.
解:【回忆】如图所示:
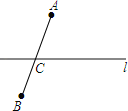
理由:两点之间线段最短;
【探索】
(1)如图所示:

理由:点到直线的距离垂线段最短;
(2)如图所示:

理由:两点之间线段最短(到OA、OC最短在AC上;到OB、OD最短在BD上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广东省茂名市第12题)已知∠A=100°,那么∠A补角为 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016浙江省舟山市第4题)13世纪数学家斐波那契的(计算书)中有这样一个问题:“在罗马有7位老妇人,每人赶着7头毛驴,每头驴驮着7只口袋,每只口袋里装着7个面包,每个面包附有7把餐刀,每把餐刀有7只刀鞘”,则刀鞘数为( )
A.42 B.49 C.76 D.77
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中随机抽取若干个学生进行调查,绘制出了两幅不完整的统计图,如图所示,请你根据图中信息解答下列问题:

(1)共抽取了多少个学生进行调查?
(2)分别求出B等级的人数和图乙中B等级所占圆心角的度数.
(3)将图甲中的折线统计图补充完整.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣3x+k与x轴交于A、B两点,与y轴交于点C(0,﹣4).

(1)k= ;
(2)点A的坐标为 ,B的坐标为 ;
(3)设抛物线y=x2﹣3x+k的顶点为M,求四边形ABMC的面积.
-
科目: 来源: 题型:
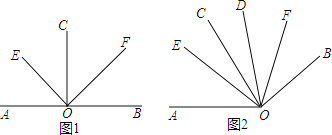
查看答案和解析>>【题目】(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= .(用含α与β的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,CA=12
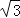 cm,BC=12cm;动点P从点C开始沿CA以2
cm,BC=12cm;动点P从点C开始沿CA以2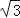 cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.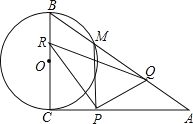
(1)∠CAB的度数是 ;
(2)以CB为直径的⊙O与AB交于点M,当t为何值时,PM与⊙O相切?
(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求S的最小值及相应的t值;
(4)是否存在△APQ为等腰三角形?若存在,求出相应的t值;若不存在请说明理由.
相关试题

