【题目】如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.

参考答案:
【答案】证明见解析.
【解析】试题分析:根据等边三角形三线合一的性质可得AD为∠BAC的角平分线,根据等边三角形各内角为60°即可求得∠BAE=∠BAD=30°,进而证明△ABE≌△ABD,得BE=BD.
试题解析:(方法1)证明:∵△ABC和△ADE都是等边三角形
∴∠DAE=∠BAC=60°∴∠EAB=∠DAC
∵AE=AD,AB=AC
∴△ABE≌△ACD(SAS)
∴BE="CD"
∵AD是△ABC的中线
∴BD="CD"
∴BE=BD
(方法2)证明:∵△ABC是等边三角形,
∴∠BAC=60°
∵AD为BC边上的中线,
∴AD平分∠BAC.
即∠BAD=∠DAC=![]() ∠BAC=30°,
∠BAC=30°,
又∵△ADE为等边三角形,
∴AE=AD=ED,且∠EAD=60°,
而∠BAD=30°,
∴∠EAB=∠EAD﹣∠BAD=30°.
∴∠EAB=∠BAD.
∴AB垂直平分DE,
∴BE=BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件:①在足球赛中,弱队战胜强队;②抛掷一枚硬币,落地正面朝上;③任取两个负数,其积大于0;④长分别为3、5、9厘米的三条线段不能围成一个三角形.其中确定事件的个数是( )个.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
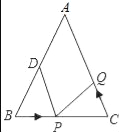
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.
(1)求证:△AEP≌△BAG;
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
(3)如图2,若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由;
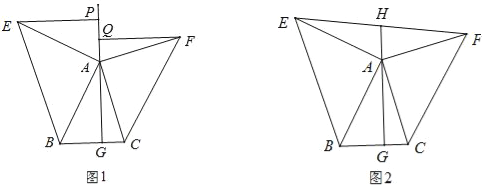
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学结合中小学生阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2所提供的信息,解答下列问题:

图1 图2
(1)在这次抽样调查中,一共抽查了多少名学生?
(2)请把折线统计图补充完整;
(3)求出扇形统计图中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1 800名,那么请你估计最喜爱科普类书籍的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】泰州梅兰芳公园开放后,前往参观的人非常多.5月中旬的一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.
(1)这里采用的调查方式是 ;
(2)求表中a、b、c的值,并请补全频数分布直方图;
(3)在调查人数里,等候时间少于40min的有 人;
(4)此次调查中,中位数所在的时间段是 ~ min.|X

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,必然事件是( )
A.6月14日晚上能看到月亮
B.早晨的太阳从东方升起
C.打开电视,正在播放新闻
D.任意抛一枚均匀的硬币,正面朝上
相关试题

