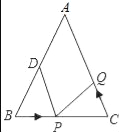
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
参考答案:
【答案】(1)①△BPD≌△CQP,理由见解析;②![]() cm/s;
cm/s;
(2)经过![]() s点P与点Q第一次在边AB上相遇.
s点P与点Q第一次在边AB上相遇.
【解析】试题分析:(1)①根据时间和速度分别求得两个三角形中的边的长,根据SAS判定两个三角形全等.
②根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;
(2)根据题意结合图形分析发现:由于点Q的速度快,且在点P的前边,所以要想第一次相遇,则应该比点P多走等腰三角形的两个腰长.
试题解析:(1)①∵t=1s,
∴BP=CQ=3×1=3cm,
∵AB=10cm,点D为AB的中点,
∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣3=5cm,
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中, 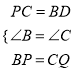 ,
,
∴△BPD≌△CQP(SAS).
②∵vP≠vQ,
∴BP≠CQ,
若△BPD≌△CPQ,∠B=∠C,
则BP=PC=4cm,CQ=BD=5cm,
∴点P,点Q运动的时间![]() ,
,
∴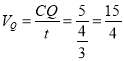 cm/s;
cm/s;
(2)设经过x秒后点P与点Q第一次相遇,
由题意,得![]() x=3x+2×10,
x=3x+2×10,
解得![]() .
.
∴点P共运动了![]() ×3=80cm.
×3=80cm.
△ABC周长为:10+10+8=28cm,
若是运动了三圈即为:28×3=84cm,
∵84﹣80=4cm<AB的长度,
∴点P、点Q在AB边上相遇,
∴经过![]() s点P与点Q第一次在边AB上相遇.
s点P与点Q第一次在边AB上相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要把一个长方体的表面剪开并展开成平面图形,至少需要剪开________条棱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在柯桥区2017年政府报告中提到,区政府大力推进“五水共治”、”五气合治“,五年来共投入资金24100000000元,将24100000000用科学记数法表示为( )
A. 2.41×1011 B. 2.41×1010 C. 24.1×1010 D. 0.241×1011
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件:①在足球赛中,弱队战胜强队;②抛掷一枚硬币,落地正面朝上;③任取两个负数,其积大于0;④长分别为3、5、9厘米的三条线段不能围成一个三角形.其中确定事件的个数是( )个.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
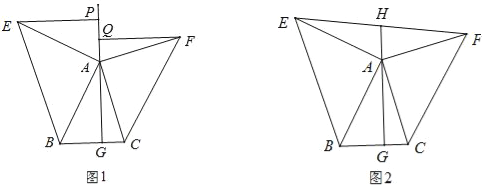
查看答案和解析>>【题目】如图1,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.
(1)求证:△AEP≌△BAG;
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
(3)如图2,若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学结合中小学生阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2所提供的信息,解答下列问题:

图1 图2
(1)在这次抽样调查中,一共抽查了多少名学生?
(2)请把折线统计图补充完整;
(3)求出扇形统计图中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1 800名,那么请你估计最喜爱科普类书籍的学生人数.
相关试题

