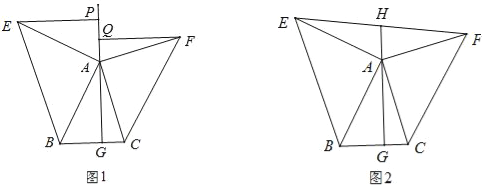
【题目】如图1,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.
(1)求证:△AEP≌△BAG;
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
(3)如图2,若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由;
参考答案:
【答案】(1)证明见解析;(2)EP=FQ,证明见解析;(3)EH=FH,理由见解析.
【解析】试题分析:(1)根据等腰Rt△ABE的性质,求出∠EPA=∠EAB=∠AGB=90°,∠PEA=∠BAG,根据AAS推出△EPA≌△AGB;
(2)根据全等三角形的性质推出EP=AG,同理可得△FQA≌△AGC,即可得出AG=FQ,最后等量代换即可得出答案;
(3)求出∠EPH=∠FQH=90°,根据AAS推出△EPH≌△FQH,即可得出EH与FH的大小关系;
试题解析:(1)如图1,∵∠EAB=90°,EP⊥AG,AG⊥BC,
∴∠EPA=∠EAB=∠AGB=90°,
∴∠PEA+∠EAP=90°,∠EAP+∠BAG=90°,
∴∠PEA=∠BAG,
在△EPA和△AGB中,
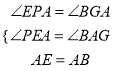 ,
,
∴△EPA≌△AGB(AAS),
(2)EP=FQ,
证明:由(1)可得,△EPA≌△AGB,
∴EP=AG,
同理可得,△FQA≌△AGC,
∴AG=FQ,
∴EP=FQ;
(3)EH=FH,
理由:如图,∵EP⊥AG,FQ⊥AG,
∴∠EPH=∠FQH=90°,
在△EPH和△FQH中,
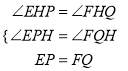 ,
,
∴△EPH≌△FQH(AAS),
∴EH=FH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在柯桥区2017年政府报告中提到,区政府大力推进“五水共治”、”五气合治“,五年来共投入资金24100000000元,将24100000000用科学记数法表示为( )
A. 2.41×1011 B. 2.41×1010 C. 24.1×1010 D. 0.241×1011
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件:①在足球赛中,弱队战胜强队;②抛掷一枚硬币,落地正面朝上;③任取两个负数,其积大于0;④长分别为3、5、9厘米的三条线段不能围成一个三角形.其中确定事件的个数是( )个.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
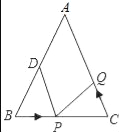
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC和△ADE是等边三角形,AD是BC边上的中线.求证:BE=BD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学结合中小学生阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2所提供的信息,解答下列问题:

图1 图2
(1)在这次抽样调查中,一共抽查了多少名学生?
(2)请把折线统计图补充完整;
(3)求出扇形统计图中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1 800名,那么请你估计最喜爱科普类书籍的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】泰州梅兰芳公园开放后,前往参观的人非常多.5月中旬的一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.
(1)这里采用的调查方式是 ;
(2)求表中a、b、c的值,并请补全频数分布直方图;
(3)在调查人数里,等候时间少于40min的有 人;
(4)此次调查中,中位数所在的时间段是 ~ min.|X

相关试题

