【题目】某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折.下表是购买量x(千克)、付款金额y(元)部分对应的值,请你结合表格:
购买量x(千克) | 1.5 | 2 | 2.5 | 3 |
付款金额y(元) | 7.5 | 10 | 12 | b |
(1)写出a、b的值,a= b= ;
(2)求出当x>2时,y关于x的函数关系式;
(3)甲农户将18.8元钱全部用于购买该玉米种子,计算他的购买量.
参考答案:
【答案】(1)5,14;(2)y=4x+2;(3)甲农户的购买量为4.2千克.
【解析】
(1)由表格即可得出购买量为函数的自变量x,再根据购买2千克花了10元钱即可得出a值,结合超过2千克部分的种子价格打8折可得出b值;
(2)设当x>2时,y关于x的函数解析式为y=kx+b,根据点的坐标利用待定系数法即可求出函数解析式;
(3)由18.8>10,利用“购买量=钱数÷单价”即可得出甲农户的购买了,再将y=18.8代入(2)的解析式中即可求出农户的购买量.
解:(1)由表格即可得出购买量是函数的自变量x,
∵10÷2=5,
∴a=5,b=2×5+5×0.8=14.
故答案为:5,14;
(2)设当x>2时,y关于x的函数解析式为y=kx+b,
将点(2.5,12)、(3,14)代入y=kx+b中,
得:![]() ,
,
解得:![]() ,
,
∴当x>2时,y关于x的函数解析式为y=4x+2.
(3)∵18.8>10,
4x+2=18.8
x=4.2
∴甲农户的购买量为:4.2(千克).
答:甲农户的购买量为4.2千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:如果y′=
 ,那么称点Q为点P的“关联点”.例如:点(5,6)的“关联点”为点(5,6),点(﹣5,6)的“关联点”为点(﹣5,﹣6).
,那么称点Q为点P的“关联点”.例如:点(5,6)的“关联点”为点(5,6),点(﹣5,6)的“关联点”为点(﹣5,﹣6).
(1)如果点A(3,﹣1),B(﹣1,3)的“关联点”中有一个在函数y= 的图象上,那么这个点是(填“点A”或“点B”).
的图象上,那么这个点是(填“点A”或“点B”).
(2)如果点N*(m+1,2)是一次函数y=x+3图象上点N的“关联点”,求点N的坐标.
(3)如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,其“关联点”Q的纵坐标y′的取值范围是﹣4<y′≤4,那么实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图边长为1的正方形ABCD被两条与边平行的线段EF、GH分割为四个小矩形,EF与GH交于点P
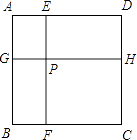
(1)若AG=AE,证明:AF=AH;
(2)若矩形PFCH的面积,恰矩形AGPE面积的两倍,试确定∠HAF的大小;
(3)若矩形EPHD的面积为 ,求Rt△GBF的周长.
,求Rt△GBF的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=
 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=  的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.﹣4
B.4
C.﹣2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)将图②中的阴影部分面积用2种方法表示可得一个等式,求等式。
(2)若m+2n=7,mn=3,利用(1)的结论求m﹣2n的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在9×9的正方形网格中,△ABC三个顶点在格点上,每个小正方形的边长为1.
(1)建立适当的平面直角坐标系后,若点A的坐标为(1,1),点C的坐标为(4,2),画出平面直角坐标系并写出点B的坐标;
(2)直线l经过点A且与y轴平行,写出点B、C关于直线l对称点B1、C1的坐标;
(3)直接写出BC上一点P(a,b)关于直线l对称点P1的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=
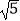 ,tanB=
,tanB= ,半径为2的⊙C,分别交AC,BC于点D,E,得到
,半径为2的⊙C,分别交AC,BC于点D,E,得到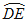 .
. 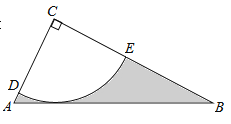
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.
相关试题

