【题目】已知:如图,![]() 、
、![]() 都是等腰三角形,且
都是等腰三角形,且![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.以下
的中点.以下![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④连
是等边三角形;④连![]() ,则
,则![]() 平分
平分![]() .正确的是( )
.正确的是( )
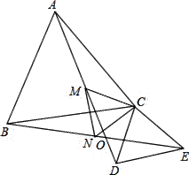
A.①②③B.①②④C.①③④D.①②③④
参考答案:
【答案】B
【解析】
①根据∠ACB=∠DCE求出∠ACD=∠BCE,证出![]() 即可得出结论,故可判断;
即可得出结论,故可判断;
②根据全等求出∠CAD=∠CBE,根据三角形外角定理得∠DOB=∠OBA+∠BAO,通过等角代换能够得到∠DOB=∠CBA+∠BAC,根据三角形内角和定理即可求出∠CBA+∠BAC,即可求出∠DOB,故可判断;
③根据已知条件可求出AM=BN,根据SAS可求出![]() ,推出CM=CN,∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断
,推出CM=CN,∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断![]() 的形状;
的形状;
④在AD上取一点P使得DP=EO,连接CP,根据![]() ,可求出∠CEO=∠CDP,根据SAS可求出
,可求出∠CEO=∠CDP,根据SAS可求出 ![]() ,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE,故可判断.
,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE,故可判断.
①正确,理由如下:
∵![]() ,
,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
又∵CA=CB,CD=CE,
∴![]() (SAS),
(SAS),
∴AD=BE,
故①正确;
②正确,理由如下:
由①知,![]() ,
,
∴∠CAD=∠CBE,
∵∠DOB为![]() 的外角,
的外角,
∴∠DOB=∠OBA+∠BAO=∠EBC+∠CBA+∠BAO=∠DAC+∠BAO+∠CBA=∠CBA+∠BAC,
∵∠CBA+∠BAC+∠ACB=180°,∠ACB=α,
∴∠CBA+∠BAC=180°-α,
即∠DOB=180°-α,
故②正确;
③错误,理由如下:
∵点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,
的中点,
∴AM= ![]() AD,BN=
AD,BN= ![]() BE,
BE,
又∵由①知,AD=BE,
∴AM=BN,
又∵∠CAD=∠CBE,CA=CB,
∴![]() (SAS),
(SAS),
∴CM=CN,∠ACM=∠BCN,
∴∠MCN=∠MCB+∠CBN=∠MCB+∠ACM=∠ACB=α,
∴![]() 为等腰三角形且∠MCN=α,
为等腰三角形且∠MCN=α,
∴![]() 不是等边三角形,
不是等边三角形,
故③错误;
④正确,理由如下:

如图所示,在AD上取一点P使得DP=EO,连接CP,
由①知,![]() ,
,
∴∠CEO=∠CDP,
又∵CE=CD,EO=DP,
∴![]() (SAS),
(SAS),
∴∠COE=∠CPD,CP=CO,
∴∠CPO=∠COP,
∴∠COP=∠COE,
即OC平分∠AOE,
故④正确;
故答案为:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有七个数﹣1,﹣2,﹣2,﹣4,﹣4,﹣8,﹣8将它们填入图1(3个圆两两相交分成7个部分)中,使得每个圆内部的4个数之积相等,设这个积为m,如图2给出了一种填法,此时m=64,在所有的填法中,m的最大值为_____.
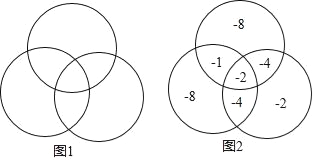
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=1cm
(1)求AC的长
(2)若点E在直线AD上,且EA=2cm,求BE的长

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知将一副三角板(直角三角板
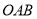 和直角三角板
和直角三角板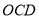 )的两个顶点重合于点
)的两个顶点重合于点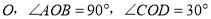 .
.
(1)如图1,将直角三角板
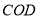 绕点
绕点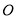 逆时针方向转动,当
逆时针方向转动,当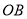 恰好平分
恰好平分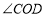 时,
时,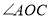 的度数是 _.
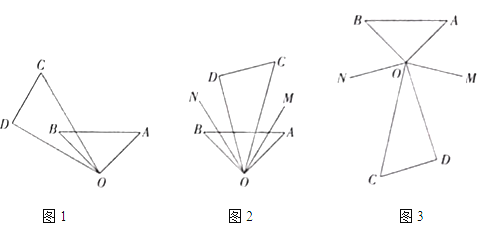
的度数是 _.(2)如图2,当三角板
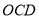 摆放在
摆放在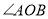 内部时,作射线
内部时,作射线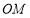 平分
平分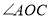 ,射线
,射线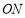 平分
平分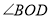 ,如果三角板
,如果三角板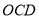 在
在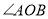 内绕点
内绕点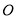 任意转动,
任意转动,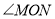 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
的度数是否发生变化?如果不变,求其值;如果变化,说明理由.(3)当三角板
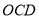 绕点
绕点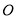 继续转动到如图3所示的位置时,作射线
继续转动到如图3所示的位置时,作射线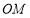 平分
平分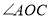 ,射线
,射线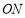 平分
平分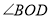 ,请你求出此时钝角
,请你求出此时钝角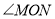 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】按要求解方程.
(1)y(y-2)=3y2-1(公式法); (2)(2x-1)2-3(2x-1)+2=0(因式分解法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节前,安徽黄山脚下的小村庄的集市上,人山人海,还有人在摆“摸彩”游戏,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1~20号)和1只红球,规定:每次只摸一只球.摸前交1元钱且在1~20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元.
(1)你认为该游戏对“摸彩”者有利吗?说明你的理由.
(2)若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
相关试题

